什麼是CAPM:深入解析資本資產定價模型,搞懂投資預期報酬與風險的奧秘
欸,你是不是也遇過這種情況?小明最近想投資股票,看著滿手資料,有時覺得這支股票好像不錯,但又說不出個所以然,不知道到底該期待多少報酬,更別提怎麼衡量風險了。他常常問:「到底我投資這筆錢,合理的預期報酬應該是多少?這風險又該怎麼評估呢?」這時候,我們今天的主角——資本資產定價模型(Capital Asset Pricing Model,簡稱CAPM)就派上用場了!
快速回答:什麼是CAPM?
說穿了,CAPM就是一個在金融領域被廣泛使用的模型,它主要在幫我們估算單一資產(比如某支股票)或整個投資組合的預期報酬率。它最核心的概念就是:資產的預期報酬,應該要跟它所承擔的「系統性風險(Systematic Risk)」成正比。換句話說,你承擔的風險越高,你就應該期待越高的報酬,反之亦然。這個模型試圖解釋為什麼有些股票的報酬率高,有些則低,並給出一個衡量「合理」報酬的基準。
今天這篇文章,就讓我來帶你深入淺出地好好認識一下CAPM這個玩意兒,從它的基本公式、每個組成部分的意義,到它背後的假設、實際應用,甚至它有哪些侷限性與學術界的爭議,全部給你講個清楚明白!
Table of Contents
什麼是資本資產定價模型(CAPM)?它到底想說什麼?
想像一下,你手上有一筆閒錢,想拿去投資。你當然希望賺錢,對不對?但這世界上沒有白吃的午餐,想要高報酬,通常就得承擔高風險。那麼,問題來了:我承擔了某種程度的風險後,到底該期待多少報酬才算「合理」呢?CAPM就是為了回答這個問題而誕生的。
CAPM模型是由美國經濟學家William F. Sharpe、John Lintner和Jan Mossin在1960年代獨立發展出來的。它基本上告訴我們,投資人為承擔「系統性風險」所獲得的補償,應該要反映在該資產的預期報酬率上。什麼是系統性風險?簡單來說,就是那些無法透過分散投資來消除的風險,像是經濟衰退、通貨膨脹、利率變動、戰爭等等,這些風險會影響整個市場,你就算買了一百支不同的股票,這些風險一樣會對你的投資組合造成影響。
CAPM假設投資人都是理性的,他們在做投資決策時,只會考慮兩件事:資產的預期報酬率和它的風險(通常用標準差來衡量)。在這樣的假設下,所有投資人都會選擇最佳的風險-報酬組合。而CAPM的目標,就是幫我們找出任何特定資產或投資組合的「預期報酬率」。
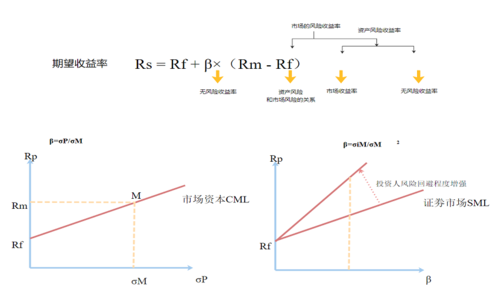
它的核心公式長這樣:
E(R_i) = R_f + β_i * (E(R_m) – R_f)
這條公式乍看之下可能有點複雜,但別擔心,我會一個蘿蔔一個坑,幫你把每個符號都解釋清楚。
CAPM公式拆解:每個變數都藏著大學問!
我們把公式的每個部分都拿出來仔細瞧瞧,你會發現,每一個變數的選取和估計,都直接影響到最終的預期報酬率計算結果。
1. 無風險利率 (R_f):那個穩穩的報酬率
E(R_i) = R_f + β_i * (E(R_m) – R_f)
這裡的 R_f 代表的就是「無風險利率」(Risk-Free Rate)。顧名思義,這是一個理論上「沒有任何風險」的投資所能獲得的報酬率。現實世界中,當然沒有絕對「無風險」的投資,因為就算把錢存銀行,還是有通膨的風險,甚至銀行倒閉的風險(雖然很低)。
不過呢,在金融實務上,我們通常會選取那些「信用等級最高」且「流動性極佳」的政府短期公債殖利率來代表無風險利率。為什麼?因為大家普遍認為,一個主權政府(特別是像美國、德國、日本這樣的大國)違約的機率非常非常低,低到可以忽略不計。
-
怎麼選?
- 在台灣,我們通常會參考台灣政府發行的短期公債(例如1年期或10年期公債)的殖利率。
- 如果是評估國際資產,或公司在全球市場募資的股權成本,很多時候會參考美國財政部發行的短期國庫券(T-bills)或長期公債(Treasuries)的殖利率。畢竟美元是全球儲備貨幣,美國公債被視為全球最安全的資產之一。
- 選多久的年期? 這也是個問題!如果你要評估的是一個為期5年的投資計畫,理論上應該選取5年期的公債殖利率。但實務上,很多人會直接用10年期公債殖利率,因為它的流動性比較好,也常被視為是反映長期資金成本的指標。這其實沒有一個絕對標準答案,通常會依據分析的標的、時間長短以及市場慣例來決定,但務必確保前後一致性。
對我來說,選擇無風險利率時,最重要的是要符合你的分析目的,並且要合理。你不能隨便抓一個數字就說它是無風險利率,那肯定會讓你的模型失去說服力。
2. Beta (β_i):衡量單一資產對市場的敏感度
E(R_i) = R_f + β_i * (E(R_m) – R_f)
接下來這個 β_i (Beta值),可以說是CAPM模型裡最核心、也最常被討論的變數了!它代表了單一資產(或投資組合)相對於整體市場的「系統性風險」衡量指標。換句話說,它告訴我們,當整個市場波動一個百分點的時候,我這支股票會跟著波動多少個百分點。
-
Beta值的意義:
- β = 1: 這表示該資產的風險程度與整個市場的平均風險一致。當市場上漲10%時,這支股票預期也會上漲10%;市場下跌10%時,它也可能下跌10%。
- β > 1: 表示該資產的風險程度高於市場平均。這類股票通常被稱為「攻擊型股票」。例如,如果β = 1.5,當市場上漲10%時,這支股票預期可能上漲15%;市場下跌10%時,它可能下跌15%。這種股票對市場變化比較敏感,波動性比較大。
- β < 1 (且 > 0): 表示該資產的風險程度低於市場平均。這類股票通常被稱為「防禦型股票」。例如,如果β = 0.5,當市場上漲10%時,這支股票預期只會上漲5%;市場下跌10%時,它可能只下跌5%。這種股票對市場變化比較不敏感,波動性相對較小。
- β = 0: 理論上,這表示該資產的報酬與市場波動完全無關。例如無風險資產。
- β < 0: 這種情況比較少見,但確實存在。它表示該資產的報酬與市場呈現「反向」關係。當市場上漲時,它可能下跌;市場下跌時,它可能上漲。例如,某些避險性質的商品或衍生性金融工具。
-
Beta值的計算:
Beta值通常是透過統計分析,也就是迴歸分析(Regression Analysis)來計算的。我們會觀察一支股票過去一段時間的報酬率,與同期整體市場(通常用一個綜合指數,比如台灣加權指數、S&P 500指數等)的報酬率之間的關係。
公式通常寫成:
β_i = Cov(R_i, R_m) / Var(R_m)
其中:
- Cov(R_i, R_m) 是資產 i 的報酬率與市場報酬率之間的協方差(Covariance),它衡量了兩者共同變動的程度。
- Var(R_m) 是市場報酬率的變異數(Variance),它衡量了市場報酬率的波動程度。
簡單來說,就是看這支股票跟大盤的報酬率變動方向是不是一致,變動幅度又如何。
-
Beta的實務挑戰與我的看法:
雖然Beta很有用,但在實務上估計Beta其實很有挑戰性。第一個問題是「數據區間」的選擇。到底要用過去一年的數據、三年、五年,還是更長?不同的時間區間,算出來的Beta值可能天差地遠。再來,「頻率」也很重要,是用日報酬率、週報酬率還是月報酬率來計算?這些選擇都會影響Beta的穩定性。
還有,Beta值並不是固定不變的。一家公司的業務模式、市場競爭環境、財務槓桿程度都會改變,這些變化都可能讓它的Beta值在未來發生變化。所以,我們看到的Beta值,其實是「過去」的數據。用過去的數據來預測未來,這本身就是一個假設。
在我看來,Beta雖然重要,但它更像是一個「指南針」,而不是精確的「GPS」。它告訴你大概的方向和敏感度,但你不能完全依賴它,還得結合對公司基本面的了解和未來的展望來綜合判斷。
3. 市場風險溢酬 (E(R_m) – R_f):市場給你的額外獎勵
E(R_i) = R_f + β_i * (E(R_m) – R_f)
公式裡的最後一個部分,就是 (E(R_m) – R_f),這就是「市場風險溢酬」(Market Risk Premium,簡稱MRP)。這個概念也很有趣,它代表的是投資整個市場(而非單一無風險資產)所能獲得的「額外」報酬。換句話說,你願意把錢從無風險資產拿出來投資風險性資產(例如股票),市場得給你多少額外的甜頭,你才覺得划算?這個額外的甜頭,就是市場風險溢酬。
- E(R_m):代表的是市場預期報酬率(Expected Market Return)。這是指投資整個市場組合,例如股票指數(如台灣加權指數、S&P 500指數),預期能夠獲得的平均報酬率。
-
如何估計市場風險溢酬?
這是一個沒有標準答案、也是最充滿爭議的環節之一!學術界和實務界對於如何估計市場風險溢酬一直有不同的看法,因為它是對「未來」的預期,沒有人能百分之百準確預測。
- 歷史數據法(Historical Approach):
最常見的方法就是看過去。我們回顧過去幾十年,股票市場的平均報酬率比無風險資產的平均報酬率高出多少。例如,如果過去50年,股市年化報酬率平均是10%,無風險利率平均是4%,那麼市場風險溢酬就是6%。
我的評論: 這種方法很簡單直觀,但有個大問題:「歷史會重演嗎?」過去的績效不代表未來。特別是經歷過大蕭條、科技泡沫、金融海嘯這些事件,市場的結構和風險偏好可能都變了。選擇不同的歷史區間,也會得到不同的結果。
- 調查法(Survey Approach):
有些機構會定期對經濟學家、基金經理、CFO們進行調查,詢問他們對未來市場風險溢酬的預期。把這些專家的預期平均起來,就作為市場風險溢酬的估計。
我的評論: 這種方法能反映當前市場參與者的情緒和共識,但「專家」也可能錯,而且這可能受到市場情緒的影響,預期過於樂觀或悲觀。
- 隱含市場風險溢酬法(Implied Market Risk Premium):
這種方法是從當前股票市場的價格,以及對未來股利或盈餘的預期,反向推導出市場預期報酬率,再減去無風險利率。這有點像解方程式,已知結果推導過程。
我的評論: 這種方法的好處是它反映了市場當前的共識,比較「即時」。但它的挑戰在於,對未來股利或盈餘的預期本身就是一個估計,可能會影響結果的準確性。
- 歷史數據法(Historical Approach):
你看,光是一個市場風險溢酬,就這麼多估計方法,每個方法都有它的道理和侷限。所以,在實務上,你很難找到一個所有人都認同的「正確」數字。通常會參考主流金融機構或學術界的平均值,或根據自己的判斷做適度調整。
CAPM背後的「完美世界」假設:為什麼它既好用又「不現實」?
任何模型,特別是經濟金融模型,為了簡化現實、便於分析,都必須建立在一些假設之上。CAPM也不例外。它的這些假設,構築了一個近乎「完美」的理論世界,但也正是這些假設,讓CAPM在現實世界中面臨諸多挑戰。
CAPM主要建立在以下幾個關鍵假設:
-
理性且厭惡風險的投資人: 假設所有投資人都是理性的,並且都厭惡風險。他們會根據預期報酬和風險來做出投資決策,並且總是追求在相同風險下獲得最大報酬,或在相同報酬下承擔最小風險。
我的評論: 喔對了,現實世界哪有這麼理性的人?人類可是充滿了各種情緒和認知偏差,追漲殺跌、聽信小道消息可是常有的事,對不對?「行為經濟學」不就在打臉這些假設嗎?
-
效率市場: 假設所有可用的資訊都能立即且無成本地被所有投資人獲取,並迅速反映在資產價格上。這意味著市場上沒有「超額報酬」的機會,所有資產都以其「公平價值」進行交易。
我的評論: 雖然市場確實有資訊快速傳播的特性,但要說它百分之百效率,資訊完全沒有成本,那可就太理想化了!內線交易、資訊不對稱還是存在的嘛。
-
同質性預期: 假設所有投資人對資產未來的報酬率、風險和相關性都有相同的預期。
我的評論: 這點就更難了。每個人對未來經濟情勢、公司表現的看法都不同,才會有買方和賣方,市場才會有交易啊!如果大家預期都一樣,那誰會賣,誰會買呢?
-
無交易成本與稅賦: 假設買賣資產沒有任何手續費、佣金、交易稅或資本利得稅等。
我的評論: 光是手續費和交易稅,就足以讓很多短線交易者頭痛了,這怎麼可能沒有呢?
-
可以無限制地以無風險利率借貸: 假設投資人可以以相同的無風險利率無限量地借入或貸出資金。
我的評論: 銀行可不是慈善機構!借錢利率通常比存款利率高,而且還有信用額度限制。這跟現實差太遠了吧!
-
資產可無限細分: 假設投資人可以買賣任意小單位的資產,例如可以買0.001股股票。
我的評論: 雖然現在零股交易越來越普及,但要達到「無限細分」,還是有段距離的。
-
單一期間模型: CAPM通常被視為一個單一期間模型,即投資者在一個決策點做出投資,並在一個未來時間點結束投資。
我的評論: 現實中的投資可是動態的,隨時都在調整,不是一個點到另一個點這麼簡單。
看到這些假設,你是不是也跟我一樣,會心一笑呢?它確實描繪了一個幾乎不可能存在的「完美」金融世界。然而,儘管這些假設與現實脫節,CAPM作為一個理論基礎,卻對我們理解資產定價、風險與報酬的關係,以及後續更複雜的金融模型發展,都產生了極為深遠的影響。它提供了一個簡潔、邏輯嚴謹的框架,讓我們能夠從一個基準點去思考問題。
實務上,我們怎麼用CAPM這把「尺」?
儘管CAPM有著「完美世界」的假設,但它在金融實務中的應用還是非常廣泛的。它就像一把有缺陷,但仍舊實用的尺子,給了我們一個衡量和比較的基準。
以下是一些CAPM在實務中的主要應用場景:
-
評估投資標的:估算預期報酬率
這是CAPM最直接的應用。當你想評估某支股票或某項專案的投資價值時,你可以用CAPM計算出它的預期報酬率。然後,你可以將這個預期報酬率與你對該資產的實際報酬預期進行比較:- 如果你的實際預期報酬率 > CAPM計算出的預期報酬率,那麼這項投資可能被「低估」了,值得考慮買入。
- 如果你的實際預期報酬率 < CAPM計算出的預期報酬率,那麼這項投資可能被「高估」了,應該避免或考慮賣出。
- 如果你的實際預期報酬率 = CAPM計算出的預期報酬率,那麼這項投資被認為是「合理定價」的。
這可以幫助投資人判斷一項投資是否值得冒險。
-
計算股權成本 (Cost of Equity, K_e):企業估值與資本預算的核心
對於企業而言,CAPM是一個非常重要的工具,用來估計公司股東所要求的「股權成本」。股權成本是公司為其股權融資所必須支付的報酬率,也是投資人投資該公司股票所要求的最低報酬率。股權成本 (K_e) = R_f + β_i * (E(R_m) – R_f)
這個股權成本,又是計算加權平均資金成本 (Weighted Average Cost of Capital, WACC) 的關鍵組成部分。WACC是公司所有資金來源(股權和債務)的平均成本,它被廣泛用於企業估值(例如DCF模型)和資本預算決策中,作為項目的折現率。
在我過去的經驗中,做企業估值或專案評估時,WACC幾乎是必備工具,而WACC的計算又離不開CAPM來估計股權成本。這也是為什麼CAPM即便有爭議,大家還是會去學、去用的原因。
-
資本預算決策:評估新專案的門檻報酬率
當公司考慮是否投資一個新的專案(例如蓋新廠房、開發新產品)時,它需要一個「門檻報酬率」(Hurle Rate)來判斷這個專案是否值得投資。CAPM計算出的預期報酬率,就可以作為這個專案的最低可接受報酬率。如果預期這個專案能帶來的報酬率低於CAPM算出來的數值,那可能就該重新考慮了。 -
資產管理:衡量投資組合經理的表現
CAPM也可以用來評估基金經理或投資組合經理的表現。如果一個基金經理能夠持續獲得超過CAPM模型所預期的報酬率(在承擔相同風險的情況下),那麼他可能就創造了「超額報酬」,也就是所謂的 Alpha (α)。Jensen’s Alpha = 實際報酬率 – CAPM預期報酬率
這表示他的選股能力或時機把握得很好,不是光靠承擔更多系統性風險賺來的。
一步步操作:使用CAPM評估資產預期報酬的具體流程
既然CAPM這麼有用,那我們要怎麼實際操作呢?這裡給你一個清晰的步驟清單:
-
步驟一:確定無風險利率 (R_f)
- 選擇一個適當的政府公債殖利率作為無風險利率。考慮投資時間長短和市場慣例。例如,台灣企業可以選用台灣10年期公債殖利率。
- 我的建議: 盡量選擇與你的投資標的貨幣和地區相符的公債。
-
步驟二:估計資產的Beta值 (β_i)
- 收集該資產(例如某支股票)和其參考市場指數(例如台灣加權指數)過去一段時間(例如5年)的月度或季度報酬率數據。
- 使用統計軟體或Excel進行迴歸分析,將資產報酬率對市場報酬率進行迴歸,估計出Beta值。許多財經網站(如Yahoo Finance、Investing.com)也直接提供上市公司的Beta值供參考。
- 我的建議: 參考不同數據源的Beta值,並對其進行合理性判斷。考慮公司業務變動對未來Beta的影響。
-
步驟三:估計市場預期報酬率 (E(R_m))
- 這通常是最困難的部分。你可以參考歷史數據(例如過去幾十年股市的平均報酬率),或者參考知名研究機構或專家的預期。
- 我的建議: 不要過度依賴單一數據源,可以取多個數據源的平均值,或自行判斷一個合理的區間。
-
步驟四:計算市場風險溢酬 (E(R_m) – R_f)
- 將步驟三估計的市場預期報酬率減去步驟一確定的無風險利率,就得到了市場風險溢酬。
-
步驟五:代入CAPM公式計算預期報酬率 (E(R_i))
- 將以上所有估計的數值代入公式:
E(R_i) = R_f + β_i * (E(R_m) – R_f)
你就可以得到該資產在承擔其系統性風險後,所應有的預期報酬率。
- 將以上所有估計的數值代入公式:
舉個例子,假設我們要評估台積電這支股票:
- 無風險利率 (R_f) = 1.5% (台灣10年期公債殖利率)
- 台積電的Beta (β_i) = 1.2 (假設查詢到的數據)
- 市場預期報酬率 (E(R_m)) = 8% (假設根據歷史數據和專家預期)
那麼,市場風險溢酬就是:8% – 1.5% = 6.5%
台積電的預期報酬率 E(R_i) = 1.5% + 1.2 * (8% – 1.5%) = 1.5% + 1.2 * 6.5% = 1.5% + 7.8% = 9.3%
這表示,根據CAPM模型,投資台積電這支股票,在承擔其相應的系統性風險後,投資人應該期待的合理年化報酬率約為9.3%。如果台積電目前的價格暗示未來報酬率會更高,那它可能就是個不錯的投資機會;反之,則可能被高估了。
CAPM的「兩面刃」:它有哪些限制和批評?
前面我們已經提到了CAPM的一些假設與現實的脫節,這些假設正是導致其在實務應用中受到批評的主要原因。雖然CAPM是經典的理論,但它也像一把「兩面刃」,有其便利性,也有其不足之處。
1. 單一因素模型:市場風險不是唯一的「風險」
CAPM最核心的批評之一,就是它只考慮了「市場風險」(透過Beta衡量)這一個風險因素。它假定所有資產的預期報酬都只與其對市場風險的敏感度有關。但現實世界很複雜,股票的報酬率可能還會受到許多其他因素的影響,例如:
- 公司規模: 小型公司的股票報酬率普遍高於大型公司(「規模效應」)。
- 帳面市值比(Book-to-Market Ratio): 高帳面市值比(即價值股)的股票報酬率往往高於低帳面市值比(即成長股)的股票(「價值效應」)。
- 動能效應(Momentum): 過去表現好的股票,在短期內可能繼續表現良好。
這些因素在CAPM模型中是沒有被考慮進去的。許多實證研究發現,光靠Beta並不能完全解釋資產報酬率的差異,這也促成了後續多因子模型(Multi-Factor Models)的發展,例如由Eugene Fama和Kenneth French提出的三因子模型(Fama-French Three-Factor Model),就加入了規模和價值兩個因子來改進模型。
2. Beta的不穩定性與預測性問題
前面我也提過,Beta值是透過歷史數據估計出來的,它可能隨著公司業務結構、財務槓桿、甚至市場環境的變化而改變。用過去的Beta來預測未來的報酬,本身就存在很大的不確定性。
而且,在不同的計算期間和頻率下,Beta值也會有所不同。要找到一個「穩定」且「具代表性」的Beta值,其實沒那麼容易。有時候,一個公司的Beta值在很短的時間內就可能從1.0變到1.5,這會讓CAPM的預期報酬率計算變得非常不穩定。
3. 假設的非現實性
這個我們已經討論很多了,從理性投資人、效率市場、無交易成本到無風險借貸,這些假設都與真實的金融市場格格不入。這些過於理想化的假設,導致CAPM在解釋真實市場現象時,往往顯得力不從心。
4. 市場風險溢酬的估計難題
市場風險溢酬的估計是一個「藝術」多於「科學」的過程。歷史數據不一定能預示未來,而專家預期又可能受情緒影響。不同的估計方法和數據來源會產生顯著差異,這直接影響到CAPM最終的計算結果。光是這個變數的爭議,就足以讓CAPM的精確性大打折扣了。
5. 經驗數據的挑戰
許多學術研究對CAPM進行了大量的實證檢驗,結果卻褒貶不一。有些研究發現CAPM在某些市場或時間段表現尚可,但也有許多研究指出,CAPM的預測能力並不理想,甚至發現Beta與平均報酬之間沒有預期的正向關係,或者關係非常弱。這讓CAPM的實證有效性大打折扣,引發了學術界的廣泛爭議。
例如,Fama and French (1992) 在他們的經典論文”The Cross-Section of Expected Stock Returns”中,就發現Beta在解釋美國股票市場的橫截面預期報酬時,幾乎沒有解釋力,而公司規模和帳面市值比則有顯著的解釋力。這可以說是對CAPM理論的一個重大打擊。
除了CAPM,還有其他模型嗎?(簡單提及)
正是因為CAPM有這麼多限制,金融學者和實務工作者才不斷地努力,試圖發展出更貼近現實、解釋力更強的模型。最著名的就是前面提到的多因子模型。
-
Fama-French三因子模型(Fama-French Three-Factor Model):
這是CAPM最著名的擴展,由Eugene Fama和Kenneth French在1992年提出。它在CAPM的市場風險因子之外,又加入了兩個新的因子:
- 規模因子(SMB, Small Minus Big): 用來捕捉小型公司股票普遍優於大型公司股票的現象。
- 價值因子(HML, High Minus Low): 用來捕捉價值股(高帳面市值比)普遍優於成長股(低帳面市值比)的現象。
這個模型顯著提升了對股票報酬率的解釋力。
-
Fama-French五因子模型(Fama-French Five-Factor Model):
在三因子模型的基礎上,Fama和French在2015年又增加了兩個因子:
- 盈利能力因子(RMW, Robust Minus Weak): 傾向於投資高盈利能力的公司。
- 投資因子(CMA, Conservative Minus Aggressive): 傾向於投資投資較為保守的公司。
-
套利定價理論(Arbitrage Pricing Theory, APT):
這是一個更通用的多因子模型,由Stephen Ross於1976年提出。與CAPM不同的是,APT沒有指定具體的風險因子是什麼,而是認為資產的預期報酬是多個未指定宏觀經濟或市場因子的線性函數。APT的優勢在於它的假設比CAPM少,但它的挑戰在於需要識別這些潛在的風險因子。
這些模型的發展,都顯示出學術界和實務界對於更精確衡量風險和預期報酬的追求。它們雖然更複雜,但也提供了更細緻的分析框架。
常見問題 Q&A:搞懂CAPM的這些眉角!
聊了這麼多,我相信你對CAPM已經有很深入的了解了。不過,在實務操作和理解上,大家還是常常會有一些疑問。下面我整理了一些常見問題,並提供我的看法,希望能幫你解開這些「眉角」!
Q1: Beta值為負數是什麼意思?這代表什麼投資策略?
Beta值為負數,表示該資產的報酬率與市場報酬率呈現反向變動。當整體市場上漲時,這類資產的價值可能會下跌;而當市場下跌時,它的價值反而可能上漲。這種資產在投資組合中被稱為「負相關資產」或「對沖資產」。
實務中,真正的負Beta股票比較少見,但有些特定資產或金融工具可能會呈現負Beta特性。例如:
- 黃金: 在經濟不確定性高或市場恐慌時,黃金通常被視為避險資產,其價格往往逆勢上漲,可能表現出輕微的負Beta。
- 某些反向ETF或做空工具: 這些金融產品的設計目的就是為了在市場下跌時獲利,所以它們的Beta值必然是負數。
投資策略上,負Beta資產的主要用途是降低投資組合的整體風險。 如果你的投資組合大部分都是正Beta的股票(也就是跟大盤同漲同跌),適當地加入一些負Beta資產,可以在市場下跌時提供一些保護,從而降低整個組合的波動性。這是一種非常有效的分散風險策略,尤其是在熊市或經濟前景不明朗時,負Beta資產能起到「緩衝」的作用。不過,要注意的是,負Beta資產在牛市時也會拖累你的整體報酬,所以配置的比例需要仔細考量。
Q2: 無風險利率要選哪個?美國公債跟台灣公債有差嗎?
選擇無風險利率確實是個技術活!它通常會根據你的分析目標、投資標的所在市場以及時間期限來決定。美國公債和台灣公債當然有差,而且差很大!
- 分析台灣的投資標的: 如果你是在分析一家台灣的上市公司、一個在台灣的投資專案,或者一個以新台幣計價的投資組合,那麼最合理的選擇通常是台灣政府發行的公債殖利率。這反映了新台幣市場的無風險水準。通常會選擇與分析期限相近的公債,例如分析一個5年期的專案,就找台灣5年期公債殖利率。如果沒有精確對應的,10年期公債殖利率是個很常見的替代選項,因為它的流動性比較好,也被視為長期資金成本的基準。
- 分析美國或國際的投資標的: 如果你分析的是一家在美國上市的公司(例如Google、Apple),或是一個以美元計價的國際投資組合,那麼毫無疑問應該使用美國財政部發行的公債殖利率。美國公債被視為全球最安全的資產之一,其殖利率是全球資金成本的重要參考指標。同樣地,會根據分析期限選擇對應的美國國庫券(短期)或長期公債。
- 貨幣匹配原則: 最重要的原則是「貨幣匹配」。如果你評估的資產或專案的現金流是以美元計價的,那麼無風險利率就應該使用美元計價的無風險利率;如果是新台幣計價,就用新台幣計價的無風險利率。否則,你就會混淆不同貨幣的風險和報酬,導致結果失真。
簡而言之,沒有哪個公債是「萬用」的,你得根據具體情境來選擇最合適的,這也是做金融分析時一個很重要的判斷力考驗。
Q3: CAPM計算出來的預期報酬率,是不是就是我實際會賺到的錢?
這個問題問得太好了!答案很明確:不,CAPM計算出來的預期報酬率,並不等於你實際會賺到的錢。
讓我這麼說吧,CAPM給你的,是一個「理論上」的、在承擔特定系統性風險下「應該」獲得的「合理」報酬率。它是一個衡量標準,一個基準線。
實際的投資報酬率會受到太多因素的影響,包括:
- 非系統性風險(Unsystematic Risk): 也就是公司特有風險,像是管理層決策失誤、新產品失敗、勞資糾紛等等。這些風險是CAPM模型沒有考慮進去的。
- 市場情緒和噪音: 短期的市場波動常常受到投資人情緒、新聞事件等「噪音」影響,這些都不是CAPM能預測的。
- 經濟週期: 宏觀經濟的起伏對實際報酬有巨大影響。
- 模型假設的偏離: 前面講的那些CAPM的理想化假設,在現實中都不成立,這也會導致模型預測與實際結果之間的差距。
- 估計的誤差: 無論是Beta值還是市場風險溢酬,它們本身都是估計值,存在誤差區間,這也會影響最終預期報酬率的準確性。
所以,你可以把CAPM當作一個「參考點」,它告訴你這個風險等級的資產,在長期來看,大概應該能給到多少報酬。但實際操作時,你還需要結合基本面分析、技術分析,以及對宏觀經濟的判斷,才能做出更全面的投資決策。不要盲目相信模型給出的單一數字,那只是一個理論值。
Q4: CAPM適合所有類型的資產嗎?
嚴格來說,CAPM主要被設計用來評估股票或股票型投資組合的預期報酬率。因為它的核心概念是基於「市場風險」(通常由股票市場指數代表)來衡量系統性風險。
對於其他類型的資產,它的適用性就沒那麼直接了:
- 債券: 債券的定價模型通常更關注其信用風險、利率風險和流動性風險,並有專門的債券定價模型。雖然高收益債券可能與股票市場有一定關聯性,但直接套用CAPM並不理想。
- 房地產: 房地產的報酬率受地理位置、政策、市場供需、租金收入等多種因素影響,且流動性較差。用CAPM來評估房地產的預期報酬,會比較牽強,通常會用其他估值方法。
- 期貨、選擇權等衍生性金融商品: 這些商品的定價有其專門的模型(例如Black-Scholes模型),因為它們的報酬率結構非常複雜,與底層資產的關係也非線性。
- 私募基金、創投等非上市公司股權: 對於這類資產,由於缺乏公開交易數據,Beta值很難直接計算。通常會採用類似產業上市公司的Beta(即「去槓桿Beta」和「再槓桿Beta」)來估計,然後進行調整。這種情況下,CAPM還是有用,但需要更多的估計和調整工作。
所以,CAPM不是萬能的。它在公開交易的股票市場中表現最好,但在其他資產類別上,要嘛不適用,要嘛需要進行大量的調整和假設,這會增加分析的複雜性和不確定性。
Q5: 如果Beta值是0,代表什麼意思?
如果一支資產的Beta值是0,這意味著它的報酬率與整體市場的波動完全沒有相關性。換句話說,無論市場是漲是跌,漲多跌少,這支資產的報酬都不受影響。
在CAPM公式中,如果Beta = 0:
E(R_i) = R_f + 0 * (E(R_m) – R_f)
E(R_i) = R_f
這表示,一個Beta值為0的資產,其預期報酬率應該就等於無風險利率(R_f)。這其實很好理解,因為它沒有承擔任何系統性風險,所以投資者不應該期待獲得任何風險溢酬,就只能得到與無風險資產一樣的報酬。
在現實世界中,很少有資產的Beta值能夠精確地等於0。理論上,無風險資產(例如短期國庫券)的Beta值應該是0。但在實務上,即使是國庫券,其殖利率也可能受到宏觀經濟因素影響,與股市的表現並非完全獨立。不過,如果我們找到一個Beta值接近0的資產,它在投資組合中的作用就是提供一個穩定的報酬來源,並且能夠有效地降低整個投資組合的波動性,因為它不會跟隨大盤起舞。這對追求穩定性、規避市場風險的投資者來說,可能具有一定的吸引力。
我的心得:CAPM,一套你必須懂,但不能盲信的工具
講到這裡,我相信你已經對「什麼是CAPM」有非常全面的理解了。從它的核心公式、每個變數的意義,到它背後的理想化假設,以及在實務中的應用和它所面臨的批評,我們都一一剖析了。
在我看來,CAPM就像是金融學領域的一塊里程碑,它簡潔而優雅地建立起風險與報酬之間的理論關係。它告訴我們,投資的報酬,其實是為了彌補你承擔的「時間價值」和「系統性風險」。光是這一點,就已經非常有價值了!它為後續更複雜的資產定價模型奠定了堅實的基礎,也訓練了我們理解市場風險的思維模式。
但同時,我們也不能盲目地將CAPM奉為圭臬。它的那些「完美世界」假設,讓它在解釋真實市場行為時,常常顯得力不從心。Beta值的估計不穩定、市場風險溢酬的爭議,都使得CAPM計算出來的「預期報酬率」更像是一個參考區間,而不是一個精確的數字。
所以,我的建議是:你一定要懂CAPM,但你更要懂得它的侷限性。 把它當作一個思考問題的框架,一個分析的起點,而不是唯一的答案。在實際投資決策時,除了CAPM的量化分析,你更需要結合對公司基本面的深入研究、產業趨勢的判斷、宏觀經濟的分析,甚至是你自己的風險承受能力和投資目標。畢竟,投資是一門藝術與科學的結合,沒有一個模型能夠完美解釋一切。
搞懂CAPM,讓你在面對複雜的金融市場時,多了一把衡量的尺子,少了一份盲目。這,就是它最大的價值所在。