長方體展開圖有幾種？深入探討其種類、結構與實用應用

你是不是也曾經跟我一樣，在課堂上被老師突然問到：「各位同學，長方體的展開圖到底有幾種呢？」或是做美勞作業時，為了剪裁一個完美的紙盒，卻怎麼也理不出頭緒？那種既好奇又有點手足無措的感覺，我可太明白了！

長方體展開圖的數目：11種經典型態

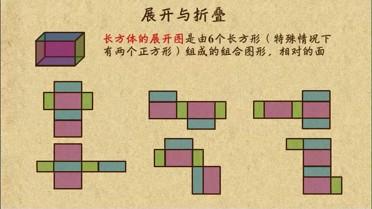
其實啊，這個問題看似簡單，背後卻蘊含著豐富的幾何學奧秘呢！一個標準的長方體，它的展開圖在經過嚴謹的數學推算與分類後，總共有 11 種不同的基本型態喔！沒錯，就是 11 種，不多不少。這可是數學家們經過系統性地排列組合與排除重複後，得出的唯一正解。這些展開圖，每一種都能夠透過摺疊，完美地構成一個完整的長方體，不多不少，不重疊不遺漏。

什麼是「長方體展開圖」？從平面到立體的奇妙旅程

在我們深入探討這 11 種展開圖之前，讓我們先來搞清楚到底什麼是「長方體展開圖」吧！簡單來說，一個長方體的展開圖，就是將這個立體的長方體，沿著它的一些邊緣剪開，然後攤平在一個平面上所形成的圖形。想像一下你把一個紙箱拆開，攤平後所得到的形狀，那就是它的展開圖了。

一個長方體有六個面，這六個面分別是三個不同尺寸的矩形，而且每種尺寸的矩形各有兩個。當我們把它攤平時，這六個面會以各種不同的方式相連。而一個「有效」的長方體展開圖，必須要符合幾個關鍵的條件：

• 所有面都必須包含： 展開圖必須包含長方體所有的六個面。
• 可以完美摺疊： 當這些平面圖形沿著它們的連接邊摺疊起來時，必須能夠精確地形成一個沒有重疊、沒有空隙的完整長方體。
• 不能有重複： 如果一個展開圖經過旋轉或翻轉後，能與另一個展開圖完全重合，那麼它們就算作同一種，不能重複計算。

理解了這些基本概念，我們就能更好地欣賞這 11 種展開圖的獨特之處了！這就像是解開一個空間謎題，把立體的結構用平面的語言來表達，真的很有趣呢！

揭秘 11 種長方體展開圖的奧秘與結構

找出這 11 種展開圖，其實就像玩拼圖一樣，需要一點耐心和空間想像力。它們之所以能夠被歸納為 11 種，是因為數學家們利用系統性的方法，將所有可能的六個矩形平面排列組合，然後篩選出那些能實際摺疊成長方體，並且互不重複的圖形。

為了更清晰地理解這 11 種展開圖，我們可以想像長方體的六個面：兩組相對的頂面和底面，以及四個側面。這些展開圖的變化，主要就來自於這六個面如何彼此連接。大部分的展開圖，都可以想像成有一個「主幹」或「骨架」，通常是由四個側面連成一排，然後頂面和底面「掛」在它的兩側。

長方體展開圖的分類與辨識

要全面地理解這 11 種，我們可以用一個簡單的策略來進行分類：觀察「中間的連續面數」以及「頂面與底面的位置」。最常見的展開圖通常以四個面排成一列（這四個面可以是長方體的側面），然後另外兩個面（頂面和底面）分別附著在這一列的上下兩側。

以下我將嘗試用文字描述這 11 種展開圖的典型配置，為了方便理解，我們可以用數字來表示連續的平面數量，例如「1-4-1」代表一個面、四個面、一個面的排列。不過請注意，這只是一種描述方式，重點還是要能夠在腦海中「摺疊」起來喔！

1. 1-4-1 型 (最經典的「十字型」展開圖)

   這是最常見，也最容易被想到的類型，就像一個大寫的「T」字或十字架。想像一下，中間有四個面排成一列，而頂面和底面則分別連接在這一列的不同位置。

   • 變體一：四個面排成一列，頂面在第二個面的上方，底面在第三個面的下方。
   • 變體二：四個面排成一列，頂面在第一個面的上方，底面在第三個面的下方。
   • 變體三：四個面排成一列，頂面在第二個面的上方，底面在第四個面的下方。
   • 變體四：四個面排成一列，頂面在第一個面的上方，底面在第四個面的下方。

   這四種雖然面連接的位置不同，但都屬於「1-4-1」的基本結構，只是頂面和底面在中央四個面的位置有所調整。只要試著在腦海中把它們摺起來，你會發現它們都能完美形成長方體！

2. 2-3-1 型 (階梯狀展開圖)

   這種展開圖看起來有點像階梯，中間是連續的三個面，而另外兩個面分別接在其中的一個面上方和下方。這種配置比 1-4-1 型多了一些變化，因為頂面和底面連接的位置可以有更多選擇。

   • 變體一：三個面排成一列，一個面接在第一個面的上方，另一個面接在第三個面的下方。
   • 變體二：三個面排成一列，一個面接在第二個面的上方，另一個面接在第三個面的下方。
   • 變體三：三個面排成一列，一個面接在第一個面的上方，另一個面接在第二個面的下方。

   這三種展開圖都符合 2-3-1 的基本精神，也就是說，有兩塊面是連在一起的，中間有三塊面，然後旁邊再有一塊面。這些變體展現了如何在不改變面數分佈的情況下，調整連接點來創造新的展開圖。

3. 2-2-2 型 (Z字型或對稱型展開圖)

   這種展開圖通常呈現一種更為「分散」的感覺，像是三個「2」連在一起，或是Z字形。它們往往具有一定的對稱性。

   • 變體一：三個兩兩相連的面，排成一條彎曲的線。比如，左邊兩個面，中間兩個面，右邊兩個面，但它們不是直線排列，而是像Z字一樣。
   • 變體二：另一個是兩個面並排，中間隔一個面，再兩個面並排。

   這種結構挑戰了我們對「中間一條長軸」的慣性思維，證明了即便面之間沒有形成一條直線，也能夠巧妙地摺疊起來。

4. 3-3 型 (L型或不規則型展開圖)

   這種展開圖相對較少見，它通常是由兩個三塊面組成的「L」形狀或類似的非直線排列的塊狀。它們看起來可能沒那麼直觀，但依然能神奇地組合成一個長方體。

   • 變體一：兩個「L」形狀相互依偎，透過共同的邊緣連接起來。
   • 變體二：一個3面排成的L形，另一個3面排成的L形，但接法不同，導致外觀不同。

   這兩種類型更是考驗我們的空間想像力，它們展示了展開圖形狀的多樣性，遠不止於我們最初可能想像的「十字形」或「直線形」。

你看，光是文字描述是不是就覺得有點燒腦了呢？這也是為什麼在教學現場，通常會搭配圖形來幫助大家理解。我自己以前在學的時候，就是拿著紙板和剪刀，一個一個地剪下來、摺疊看看，才能真正消化這些概念。那種親手驗證「喔！原來這樣真的可以！」的感覺，是任何書本都給不了的。

繪製與驗證長方體展開圖的實用步驟

如果你想自己動手試試看，或者在教導孩子、學生時，以下這些步驟會很有幫助，能讓你更有系統地找出或驗證展開圖：

1. 步驟一：從「中間主幹」開始。

   先畫出一個由四個矩形側面排成一列的「主幹」。這四個面會形成長方體的側面。你可以想像這是長方體繞著一條軸展開的樣子。這會是我們展開圖的基礎結構。

2. 步驟二：策略性地安排頂面與底面。

   長方體還有兩個相對的面：頂面和底面。它們不能直接連接到「主幹」的兩端，而是必須連接在主幹的「側面」。試著將頂面和底面分別連接到主幹上不同的面，每次只移動一個面，觀察會產生什麼新的組合。
   
   舉例來說，如果中間是四個面 A-B-C-D，頂面可以連在 A 的上方、B 的上方、C 的上方或 D 的上方；底面則可以連在 A 的下方、B 的下方、C 的下方或 D 的下方。但要確保它們最終能圍合。

3. 步驟三：進行「摺疊想像」與驗證。

   這是最關鍵的一步！當你畫好一個展開圖後，請在腦海中想像，或者實際剪下來摺疊看看：

   • 邊緣是否完美對齊？ 摺疊後，所有的邊緣都應該剛好貼合，不多不少。
   • 面是否重疊？ 任何兩個面都不能在摺疊後互相重疊。
   • 是否有空隙？ 長方體摺疊後應該是一個完全封閉的立體，不能有任何開口。

   如果以上三點都符合，那麼恭喜你，你找到了一個有效的長方體展開圖！

4. 步驟四：排除重複（判斷是否「全等」）。

   這一步是區分 11 種獨特展開圖的關鍵。兩個展開圖如果透過旋轉、翻轉或鏡像後能夠完全重合，那它們就被視為同一種。這需要你仔細比對，有時候一個看似不同的圖形，只要旋轉一下，就會發現它其實就是你之前已經找到的一種。這也是為什麼找出這 11 種會有點挑戰性，因為要確保每一種都是「獨一無二」的。

我在教學生時，常常會讓他們用不同顏色的筆，把相對的面塗上相同的顏色，這樣在想像摺疊的時候，就能更容易判斷哪些面應該在長方體的對面。這是一個非常實用的技巧，也能幫助訓練大家的空間感。

為什麼只有 11 種？背後的數學拓撲學原理

為什麼偏偏是 11 種，而不是 10 種或 12 種呢？這其實是幾何學和拓撲學的一個經典問題。數學家們透過嚴謹的「窮舉法」（exhaustion method），系統地列出所有可能的組合，並利用「圖論」和「組合學」的原理，排除那些不能形成長方體，或是重複的排列組合。

這種系統性的分析確保了沒有任何一個有效的展開圖被遺漏，也沒有任何一個重複的被重複計算。這就像是把所有可能的拼圖組合都嘗試過一遍，最後發現只有這 11 種是「正確答案」。而其背後的核心概念，其實就是如何將一個三維的物體表面，以一種保留其所有連接關係的方式，投影到二維平面上，同時又要保持它的「連通性」。

這不是隨機的結果，而是數學嚴謹性下的產物。對我來說，這種從無序中找出規律、從複雜中提煉簡潔的過程，正是數學最迷人的地方啊！

長方體展開圖在生活中的應用與啟示

你可能會覺得，找出這 11 種展開圖是不是只是數學家的「閒情逸致」呢？其實不然！長方體展開圖的概念，在我們的日常生活中可是無處不在，而且發揮著重要的作用：

• 包裝設計： 最直接的應用當然就是各種盒子、紙箱的設計了！從外送餐盒、禮品包裝、到大型的貨運紙箱，設計師們都需要精確地計算展開圖，以確保材料的最有效利用、切割的便利性，以及摺疊成型後的穩固性。一個好的展開圖設計，不僅能降低成本，還能減少資源浪費。
• 建築與工程： 雖然建築物很少直接是單純的長方體，但從概念上來說，許多建築構件或預製模塊的設計，也需要從平面的板材（如鋼板、木板）切割、彎折，最終組合成三維結構。這其中的原理，與展開圖的概念異曲同工。
• 教育與認知發展： 對於學生來說，學習長方體展開圖是培養空間想像力、邏輯推理能力和問題解決能力的重要途徑。透過動手操作，將平面轉化為立體，不僅讓抽象的幾何知識變得具體可感，也激發了他們對數學的興趣。
• 藝術與設計： 有些藝術家或設計師會利用展開圖的原理，創造出有趣的紙藝作品、摺紙雕塑或創意家具。這些作品往往巧妙地運用了平面與立體之間的轉換，帶來視覺上的驚喜。

回想我小時候，因為美術課要做一個盒子，當時只知道隨便剪，常常剪得亂七八糟，不是少一塊就是多一塊，或者根本摺不起來。現在回頭看，如果當時就知道這些展開圖的奧秘，我的勞作課分數肯定會高很多吧！所以說，這不僅是書本上的知識，更是實實在在的生活智慧呢！

常見問題與深入解答

正方體展開圖跟長方體展開圖有什麼不同嗎？

這是一個很棒的問題！其實，從「拓撲結構」的角度來看，正方體和長方體的展開圖是完全相同的。換句話說，它們都只有 11 種基本型態。

為什麼會這樣呢？因為正方體可以看作是一種特殊的長方體，它的所有邊長都相等，因此所有六個面都是大小完全相同的正方形。而長方體的六個面則是由三組不同尺寸的矩形組成（每種尺寸兩個）。儘管面的形狀和尺寸不同，但它們「彼此連接的方式」以及「構成一個封閉立體的結構原理」是完全一致的。

所以，當我們討論「有幾種展開圖」時，我們主要關心的是這些面如何在平面上排列，以及它們如何透過連接邊來形成立體，而不是面的具體大小。因此，學習長方體的展開圖，也就同時掌握了正方體的展開圖了，是不是很划算呢？

怎麼確保我畫出來的展開圖是「合法」的？

要確保你畫出的展開圖是「合法」且能成功摺成長方體，有幾個關鍵的檢查點，就像你前面提到的，避免重疊和空隙。

首先，面的數量一定要正確，長方體有六個面，所以你的展開圖也必須是六個面，不多不少。其次，也是最重要的一點，就是仔細檢查相對的面。在長方體中，有三對相對的面。在展開圖中，這三對相對的面彼此之間必須至少「隔」一個面，而且不能是直接連接的。你可以嘗試用兩種方法來想像：

1. 顏色或數字標記法： 假設你的長方體有六個面，分別用 A、B、C、D、E、F 來標記。想像 A 和 F 是相對面，B 和 E 是相對面，C 和 D 是相對面。在你的展開圖上，給六個面標上這些字母。然後想像摺疊後，標記相同顏色的面是否會相對，且中間是否恰好隔開。如果摺疊後發現兩個相同顏色的面緊鄰或重疊，那這個展開圖就是錯誤的。
2. 邊緣對齊檢查： 想像你用膠帶黏合展開圖的邊緣。摺疊時，每一條邊都必須找到一個唯一的「搭檔」邊緣來對齊黏合。如果某條邊沒有搭檔，或者某條邊需要和多於一條邊黏合（這會導致重疊），那麼這也不是一個合法的展開圖。這需要一些空間想像力，但透過反覆練習，你會越來越熟練的。

為什麼有些展開圖看起來很像，卻被算成不同種？有些又被算成同一種？

這個問題觸及了判斷展開圖「是否相同」的核心概念，也就是「全等」。

當我們說兩個展開圖是「同一種」時，指的是它們在幾何學上是全等的。這意味著，如果我們將其中一個展開圖進行旋轉、翻轉（鏡像）或者平移後，它能夠完全與另一個展開圖重合。你可以想像你把一個剪好的展開圖拿起來，在桌面上轉一轉、翻個面，如果它能和另一個圖形完美疊合，那它們就是同一種。

而如果兩個展開圖，無論你怎麼旋轉、翻轉或平移，都無法讓它們完全重合，那麼它們就是不同的種類。有些展開圖可能看起來很相似，只差一個小小的面位移，但這個位移可能導致了完全不同的摺疊方式，或者形成了一個無法閉合的結構。這時候，它們就是不同的展開圖。

判斷全等需要細心和耐心，有時候甚至需要你真的剪下來，在物理空間中操作看看，才能真正理解其間的差異。這也是空間幾何學習中一個很有挑戰性，但也很有趣的部分。

我要怎麼記憶這 11 種展開圖呢？有沒有什麼訣竅？

要記憶這 11 種展開圖，與其死記硬背，不如掌握其「變化規律」和「檢查方法」。我個人認為，最有效的訣竅是：

1. 從基本款開始： 從最容易理解的「1-4-1 型」十字架展開圖開始（中間四個面連成一線，上下各一個面）。這種類型本身就有四種變體。先確保你完全理解並能畫出這幾種。
2. 「移動」的練習： 接下來，試著從一個已知的合法展開圖，輕微地「移動」其中一個面。例如，將十字架型的一個頂面從第二個面的上方，移到第三個面的上方。然後再次檢查它是否仍然是合法的，並且與之前的展開圖是否全等。這種漸進式的探索，能幫助你系統地發現新的展開圖。
3. 分類記憶： 你可以嘗試將這 11 種展開圖進行簡單的分類，例如：
   • 中間有四個面排成一列的（1-4-1 型）
   • 中間有三個面排成一列的（2-3-1 型）
   • 沒有連續四個面，甚至沒有連續三個面，呈現更分散狀態的（2-2-2 型或 3-3 型）

   透過這樣的大方向分類，可以讓記憶負擔減輕不少。

4. 動手實作： 我強烈建議你準備一些方格紙和剪刀，親自動手畫、剪、摺。實際操作的經驗，遠比你看一百遍圖片都來得深刻。當你親手將平面變成一個長方體時，你會對這些展開圖的結構有更直觀、更深刻的理解。這不只是一種記憶，更是一種能力的培養。

不要想一次就把 11 種都記下來，這很難。循序漸進，理解它們的原理和變化方式，你會發現這個過程其實充滿樂趣，而且你的空間想像力也會大大提升喔！

結語：展開圖的無限魅力

長方體展開圖這個看似簡單的幾何問題，實際上牽涉到深厚的數學原理與廣泛的實用價值。從我們課桌上的數學課本，到商店貨架上的各式包裝，甚至在更廣闊的設計與工程領域，它都默默地發揮著作用。

掌握這 11 種長方體展開圖，不僅僅是記住一個數字，更是培養我們空間想像力、邏輯推理能力的重要過程。希望這篇文章能幫助你更深入地理解長方體展開圖的奧秘，也能讓你像我一樣，從中找到幾何世界的無限魅力！下次再遇到這樣的問題，你一定能自信滿滿地給出答案，並且還能解釋得頭頭是道呢！