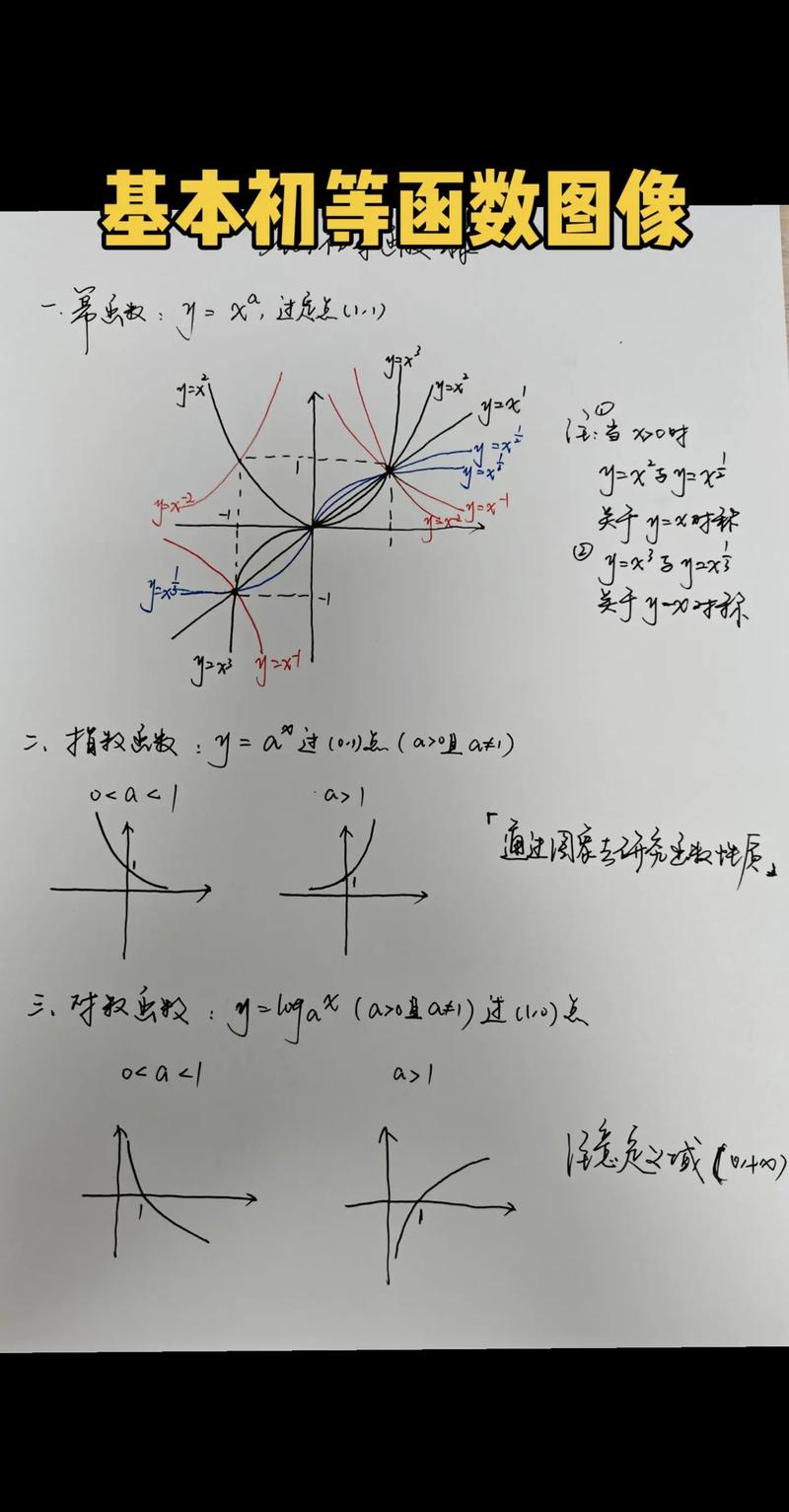
基本函數有哪些:從線性到指數,一次搞懂常見函數類型與應用
您是否曾經好奇,在浩瀚的數學世界中,那些被稱為「函數」的基本構成元素究竟有哪些?從國中、高中數學課程,到日常生活中的各種模型與預測,函數無處不在,它是理解世界運作模式的強大工具。本篇文章將深入淺出地為您解析基本函數有哪些,並詳細介紹它們的特性、通用形式及在現實生活中的廣泛應用,幫助您徹底搞懂這些數學基石!
Table of Contents
什麼是函數?函數概念的基礎定義
在我們探討基本函數有哪些之前,讓我們先建立對「函數」這個概念的清晰理解。
在數學中,函數(Function)是一種特殊的關係,它將一個集合中的每一個輸入值(通常表示為 x)唯一地對應到另一個集合中的一個輸出值(通常表示為 y 或 f(x))。簡單來說,就是「給定一個輸入,只會有一個確定的輸出」。
這個定義的核心在於「唯一性」。例如,如果我們有一個函數 f(x) = x + 2,當輸入 x = 3 時,輸出永遠都是 5。不會有時是 5,有時又是 7 的情況。在圖形上,這可以用「垂直線測試」來判斷:如果任何一條垂直線與圖形相交不超過一次,那麼這個圖形就代表一個函數。
理解函數的核心概念是掌握各種基本函數的基礎,因為它們都必須遵循這個輸入與輸出的唯一對應關係。
基本函數有哪些?九大常見類型詳細解析
當我們談論基本函數有哪些時,通常指的是在初等數學和代數中常見且具有鮮明特徵的幾種函數類型。它們不僅是更複雜函數的建構區塊,也是許多科學、工程和經濟模型的核心。以下我們將詳細介紹九種最常見的基本函數:
1. 線性函數 (Linear Function)
定義與通用形式: 線性函數是最簡單的函數類型之一,其圖形為一條直線。
通用形式為:y = mx + b 或 f(x) = mx + b
- m 代表直线的斜率(坡度),決定了線的傾斜程度和方向。
- b 代表直线的 y 截距,即直線與 y 軸相交的點。
特性:
- 圖形為一條直線。
- 變化率(斜率)是常數,表示每當 x 增加一個單位時,y 增加(或減少)的量。
- 定義域和值域均為所有實數。
實際應用:
- 計程車費率: 起跳費(b)加上每公里費用(m)乘以行駛距離(x)。
- 薪資計算: 基本月薪加上銷售獎金(基於銷售額的百分比)。
- 物體運動: 等速運動的距離與時間的關係。
2. 二次函數 (Quadratic Function)
定義與通用形式: 二次函數是最高次數為二的多項式函數,其圖形為一條拋物線。
通用形式為:y = ax² + bx + c 或 f(x) = ax² + bx + c
- a, b, c 均為常數,且 a ≠ 0。
- a 的正負決定拋物線開口方向(a > 0 開口向上,a < 0 開口向下)。
特性:
- 圖形為對稱的拋物線,有一個頂點。
- 頂點是拋物線的最高點或最低點。
- 定義域為所有實數,值域取決於頂點和開口方向。
實際應用:
- 拋體運動軌跡: 投擲物體(如籃球、水柱)在空中劃出的弧線。
- 衛星天線設計: 拋物面聚焦訊號的原理。
- 最佳化問題: 求最大利潤或最小成本的生產數量。
3. 多項式函數 (Polynomial Function)
定義與通用形式: 多項式函數是將線性函數和二次函數推廣到更高次數的形式。
通用形式為:f(x) = a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0
- a_n, a_{n-1}, …, a_0 均為常數,且 a_n ≠ 0。
- n 為非負整數,表示多項式的次數。
特性:
- 圖形是平滑且連續的曲線。
- 次數 n 決定了函數圖形的大致形狀和最多有多少個轉折點。
- 定義域為所有實數。
實際應用:
- 數據擬合: 用曲線來近似表示一組複雜的數據點。
- 工程學: 描述橋樑、道路的曲線設計。
- 經濟學: 描述供應、需求或成本的複雜關係。
4. 有理函數 (Rational Function)
定義與通用形式: 有理函數是由兩個多項式函數相除而成的函數。
通用形式為:f(x) = P(x) / Q(x)
- P(x) 和 Q(x) 均為多項式函數。
- Q(x) 不能為零。
特性:
- 圖形通常包含漸近線(垂直漸近線、水平漸近線或斜漸近線)。
- 定義域為所有實數,但必須排除使分母 Q(x) 為零的 x 值。
- 可能存在不連續點(例如,洞或垂直漸近線)。
實際應用:
- 化學: 描述化學反應中濃度隨時間的變化。
- 電學: 計算電路中的電阻、電流或電壓。
- 平均成本計算: 總成本函數除以生產數量。
5. 指數函數 (Exponential Function)
定義與通用形式: 指數函數是變數位於指數位置的函數。
通用形式為:y = b^x 或 f(x) = ab^(kx)
- b 稱為底數,且 b > 0 且 b ≠ 1。
- 如果 b > 1,函數呈現指數成長;如果 0 < b < 1,函數呈現指數衰退。
特性:
- 圖形快速增長或快速衰減。
- 總會通過點 (0, 1)(當 a=1 時)。
- 有一個水平漸近線(通常是 y=0)。
- 定義域為所有實數,值域為所有正實數。
實際應用:
- 人口增長: 描述人口數量隨時間的指數增長。
- 放射性衰變: 放射性物質半衰期的計算。
- 複利計算: 投資金額隨時間的增長。
- 傳染病擴散: 疾病在初期階段的傳播速度。
6. 對數函數 (Logarithmic Function)
定義與通用形式: 對數函數是指數函數的反函數。
通用形式為:y = log_b (x) 或 f(x) = log_b (x)
- b 稱為底數,且 b > 0 且 b ≠ 1。
- 它回答的問題是:「b 的多少次方會得到 x?」
特性:
- 圖形是其對應指數函數關於直線 y=x 的對稱。
- 總會通過點 (1, 0)。
- 有一個垂直漸近線(通常是 x=0)。
- 定義域為所有正實數,值域為所有實數。
實際應用:
- 音量衡量: 分貝(dB)的計算。
- 地震強度: 芮氏規模的計算。
- 酸鹼度: pH 值的計算。
- 資料壓縮: 在資訊科學中的應用。
7. 三角函數 (Trigonometric Functions)
定義與通用形式: 三角函數描述了直角三角形中角與邊長之間的關係,以及圓周運動的週期性。最基本的是正弦(Sine)、餘弦(Cosine)和正切(Tangent)。
通用形式為:
y = sin(x)
y = cos(x)
y = tan(x)
特性:
- 具有週期性,圖形呈現波浪狀。
- 定義域為所有實數(正切函數有例外,其定義域需要排除使分母為零的角度)。
- 值域有界限(正弦和餘弦在 [-1, 1] 之間)。
實際應用:
- 物理學: 描述聲波、光波、電流等波動現象。
- 工程學: 建築結構中的角度和力學計算。
- 天文學: 描述天體運行軌跡。
- 音樂: 樂器發出的音波振動。
8. 絕對值函數 (Absolute Value Function)
定義與通用形式: 絕對值函數的作用是將任何輸入值轉換為其非負的對應值。
通用形式為:y = |x| 或 f(x) = |x|
- 如果 x ≥ 0,則 |x| = x。
- 如果 x < 0,則 |x| = -x。
特性:
- 圖形呈現 V 形,其最低點(頂點)在原點 (0,0)。
- 定義域為所有實數。
- 值域為所有非負實數 [0, ∞)。
實際應用:
- 距離計算: 兩個數軸上點之間的距離。
- 誤差分析: 衡量測量值與真實值之間的偏差大小。
- 程式設計: 確保數值為正。
9. 分段函數 (Piecewise Function)
定義與通用形式: 分段函數的定義域被分成幾個部分,每個部分應用不同的函數規則。
通用形式為:
f(x) = { G(x) 當 x 滿足條件1
{ H(x) 當 x 滿足條件2
{ ...
特性:
- 圖形可能包含跳躍或尖點,不一定連續或平滑。
- 每個子函數在各自的定義域上表現不同。
實際應用:
- 稅率計算: 所得稅根據收入級距適用不同的稅率。
- 郵資或運費: 根據包裹重量或距離適用不同費率。
- 手機通話費: 月租費或超出特定時數後的不同計費方式。
為何理解基本函數如此重要?
掌握基本函數有哪些及其特性,不僅是數學學習的基礎,更是培養邏輯思考和問題解決能力的關鍵。這些函數是:
- 建立數學模型的核心: 無論是預測天氣、分析經濟趨勢還是設計工程結構,基本函數都能幫助我們將現實世界的複雜現象轉化為可量化的數學模型。
- 解決實際問題的工具: 從計算投資回報率到規劃最佳生產流程,函數提供了強大的分析框架。
- 深入學習進階數學的基石: 微積分、線性代數、微分方程等更高級的數學分支,都建立在對基本函數透徹理解的基礎之上。
因此,無論您是學生、工程師、科學家還是商務人士,對這些基本函數的認識和應用能力都將極大地增強您的分析能力和洞察力。
常見問題 (FAQ)
如何判斷一個關係是否為函數?
判斷一個關係是否為函數最簡單的方法是使用垂直線測試(Vertical Line Test)。在關係的圖形上,如果任何一條垂直線與圖形相交不超過一次(即最多一個交點),那麼這個關係就是函數。這確保了每個輸入值 x 都只對應一個唯一的輸出值 y。
為何指數函數和對數函數是彼此的反函數?
指數函數和對數函數是彼此的反函數,這表示它們的作用是相互抵消的。若 f(x) = b^x 是一個指數函數,則其反函數 f⁻¹(x) = log_b (x) 就是一個對數函數。這意味著 f(f⁻¹(x)) = x 且 f⁻¹(f(x)) = x。從圖形上看,它們的圖形會關於直線 y=x 對稱。
如何從現實生活中識別函數?
識別現實生活中的函數,可以從尋找具有「輸入-輸出」和「唯一對應」關係的事物著手。例如:
輸入: 購買的蘋果公斤數
輸出: 需要支付的總金額(在每公斤單價固定的情況下,總金額唯一對應公斤數,這是一個線性函數)
輸入: 銀行帳戶的年數
輸出: 帳戶中的總金額(在固定利率下,這可能是一個指數函數)
只要您能明確定義一個輸入導致一個且只有一個確定的輸出,那它就可能是一個函數關係。
為何有些函數的圖形會有不連續點?
函數圖形出現不連續點通常有幾種情況:最常見的是有理函數(當分母為零時,函數無定義,產生垂直漸近線或洞)和分段函數(在不同區間的交界處,若子函數的值不匹配,就會產生跳躍式的斷裂)。不連續點表示在該輸入值處,函數的行為或定義發生了改變。
為何理解基本函數對學習進階數學很重要?
理解基本函數是學習進階數學的基礎,因為它們是構成所有更複雜數學概念的「積木」。例如,微積分中的導數和積分,本質上都是在分析這些基本函數的變化率和累積效應。沒有對線性、二次、指數和三角函數等基本類型的紮實掌握,將難以理解其在微積分、微分方程、線性代數等領域的應用與推導。