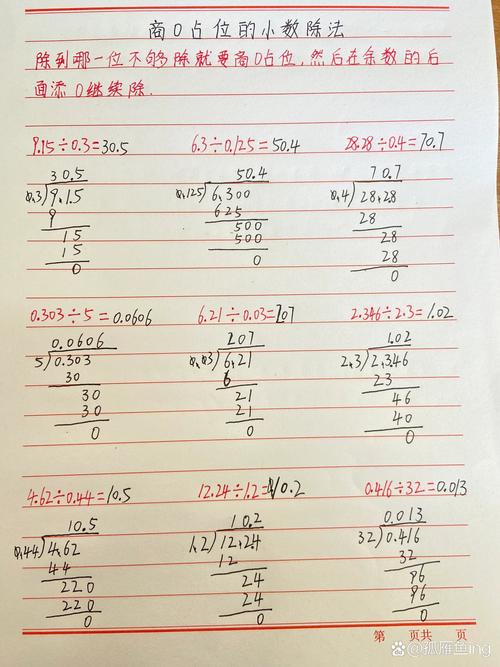
小數點除法:從原理到實戰,一次搞懂所有疑惑
Table of Contents
深入淺出:全面解析小數點除法
在數學世界中,小數點除法是許多人學習過程中的一大挑戰,卻也是日常生活、科學計算、財務管理等領域不可或缺的基礎技能。無論是計算每公斤的單價、分配有限資源,或是理解比例關係,小數點除法的應用隨處可見。許多學習者在面對小數點移動、商數定位等問題時感到困惑。本文將深入淺出,帶您完整掌握小數點除法的核心概念、步驟、特殊情況處理,並提供實用範例,讓您輕鬆告別數學恐懼,自信應對各類小數點除法問題。
核心概念:什麼是小數點除法?
小數點除法,顧名思義,就是涉及小數的除法運算。它與整數除法有著相同的本質:找出一個數(商數)被另一個數(除數)除後,能從被除數中取走多少個除數。簡單來說,就是將一個帶有小數點的數(被除數)分成若干份,每份的大小由另一個數(除數)決定。
理解小數點除法的關鍵在於,我們通常會將其轉化為更熟悉的整數除法來進行。這種轉化是透過調整除數和被除數的小數點位置來實現的,目的是為了簡化計算過程,同時確保運算的結果(商數)保持不變。
小數點除法的基本步驟:一步步搞懂
掌握小數點除法最有效的方法就是遵循一套清晰的步驟。以下我們以一個範例來詳細說明每一步驟,例如:5.75 ÷ 0.5
第一步:將除數化為整數
這是小數點除法中最核心且關鍵的一步。目的是將除數(本例為 0.5)轉換成一個整數,這樣我們就可以像進行傳統的整數除法一樣來計算了。
-
觀察除數的小數點位置: 除數 0.5 的小數點後有一位數字。
-
向右移動小數點: 為了將 0.5 變成整數 5,我們需要將其小數點向右移動 1 位。
-
重要原則: 除數的小數點移動了多少位,被除數的小數點也必須向右移動相同的位數。這是為了保持除法運算中「比例」不變的原則。
範例應用:
將除數 0.5 的小數點向右移動 1 位,變為 5。
第二步:調整被除數的小數點
根據第一步的原則,除數的小數點向右移動了幾位,被除數的小數點也必須向右移動相同的位數。如果被除數的位數不足,需要補零。
-
觀察被除數的小數點位置: 被除數 5.75 的小數點後有兩位數字。
-
向右移動小數點: 由於除數的小數點向右移動了 1 位,被除數 5.75 的小數點也必須向右移動 1 位。
範例應用:
將被除數 5.75 的小數點向右移動 1 位,變為 57.5。
至此,原來的除法算式 5.75 ÷ 0.5 就被轉化為 57.5 ÷ 5。
第三步:進行整數除法
現在,您可以像進行一般的長除法一樣,計算調整後的被除數(57.5)除以調整後的除數(5)。
範例應用:
進行 57.5 ÷ 5 的長除法運算:
11.5
_______
5 | 57.5
5
—
7
5
—
2 5
2 5
—-
0
第四步:商數小數點的定位
在長除法計算過程中,當您進行到被除數原本小數點的位置時,就需要在商數(結果)中對應的位置點上小數點。
範例應用:
在 57.5 ÷ 5 的計算中,當您將 5 除以 5 得到商數 1,並將 7 除以 5 得到商數 1,餘數 2 後,接下來要處理的是 57.5 的小數點後的「5」。在商數中,您需要將小數點放在 11 的後面,然後繼續計算 25 除以 5 得到 5。因此,商數為 11.5。
第五步:除不盡的處理方式
有時,除法運算可能不會得到一個有限小數。在這種情況下,您可能需要根據要求進行四捨五入,或是將結果表示為循環小數。
例如:10 ÷ 3
-
無限循環小數: 10 除以 3 等於 3.3333…,這是一個無限循環小數。通常會用「3.3」或「3.3」來表示。
-
四捨五入: 如果要求將結果四捨五入到特定的小數點位數,例如到小數點後第二位,那麼 3.333… 就會變成 3.33。
-
加零繼續除: 當被除數除到最後剩下餘數,且您希望得到更精確的小數點結果時,可以在餘數後面補零,繼續進行除法運算。例如 5 ÷ 4 = 1 餘 1,補零後變 10 除以 4,得 2 餘 2,再補零變 20 除以 4,得 5,最終結果為 1.25。
特殊情況與注意事項
雖然基本步驟適用於大多數情況,但小數點除法仍有一些特殊情況需要特別留意。
除數為整數但被除數為小數
這種情況相對簡單,因為您不需要移動除數的小數點。只需將被除數的小數點直接對齊商數的小數點位置,然後進行正常的整數除法即可。
範例: 12.8 ÷ 4
直接進行長除法:12 ÷ 4 = 3,接著處理小數點後的 8。在商數 3 的後面加上小數點,然後 8 ÷ 4 = 2。結果為 3.2。
被除數小於除數
當被除數小於除數時,商數會是一個小於 1 的小數(即 0.xxx…)。這時,您需要在商數中先寫 0,並將小數點點上,然後在被除數後面補零繼續計算。
範例: 0.5 ÷ 2
0 除以 2 等於 0,點上小數點。然後考慮 5 除以 2,不足,補零變成 50,50 除以 20 得到 2 餘 10,再補零變成 100 除以 20 得到 5。結果為 0.25。
除數或被除數末尾有零
在移動小數點時,如果遇到末尾有零的情況,應確保小數點移動的位數正確,必要時在末尾補零。
範例: 120 ÷ 0.3
將除數 0.3 的小數點向右移動 1 位,變為 3。
被除數 120 也需向右移動 1 位。由於 120 是整數,可以看作 120.0,向右移動 1 位後需要補零,變成 1200。
現在運算變為 1200 ÷ 3。結果為 400。
結果為循環小數
某些除法運算會產生無限循環小數,例如 1 ÷ 3 或 2 ÷ 7。在計算時,您會發現餘數重複出現,此時商數中的某個或某些數字也會重複出現。
-
表示方式: 通常會用一個點或一條線來標示循環節,例如 1 ÷ 3 = 0.3 或 2 ÷ 7 = 0.285714。
-
實際應用: 在實際應用中,通常會要求將結果四捨五入到指定的小數點位數。
應用情境舉例
小數點除法在日常生活中無處不在,以下是一些常見的例子:
計算每單位價格
如果你在超市買了一包 1.5 公斤的蘋果,花了 90.75 元,那麼每公斤蘋果的價格就是 90.75 ÷ 1.5 = 60.5 元。
分配資源
你有 25.5 公升的汽油,如果你的車子每公升汽油可以跑 8.5 公里,那麼這桶汽油可以讓你跑多遠?25.5 ÷ 8.5 = 3 公里。
計算平均值
某公司去年總營收為 1250 萬元,共有 12.5 名員工(考慮兼職員工的比例),平均每名員工的營收貢獻是多少?1250 ÷ 12.5 = 100 萬元。
學習小數點除法的常見挑戰與解決方案
許多人在學習小數點除法時會遇到以下挑戰,但這些都有解決之道:
小數點移位錯誤
挑戰: 忘記將被除數的小數點移動相同的位數,或移動方向錯誤。
解決方案: 始終記住「除數化整數,被除數跟著移」的口訣。在動手計算前,先在紙上用箭頭標示小數點的新位置,確保兩者同步。
整數除法計算失誤
挑戰: 雖然轉化成了整數除法,但基本的長除法計算仍然會出錯。
解決方案: 加強基礎整數除法的練習。可以從簡單的整數除法題目開始,逐步增加難度。使用九九乘法表或乘法口訣來輔助計算。
商數小數點定位錯誤
挑戰: 完成整數除法後,忘記在商數中正確放置小數點。
解決方案: 在進行長除法時,當被除數的小數點位置被「越過」時,立即在商數對應位置點上小數點。可以將小數點先點好,作為提醒。
除不盡的處理
挑戰: 不知道何時停止計算,或不清楚如何表示循環小數,也不懂得如何四捨五入。
解決方案: 理解題目要求,是要求精確值、四捨五入到某一位數,還是將結果表示為分數。對於循環小數,掌握標記符號的使用。
實用練習與工具推薦
「熟能生巧」是掌握小數點除法的最佳途徑。以下是一些練習和工具推薦:
-
多做練習題: 從課本、參考書或線上資源尋找不同難度的練習題。初期可從簡單的數字開始,逐步挑戰更複雜的題目。
-
使用線上計算器輔助: 在完成手算後,使用線上計算器或手機計算器來驗證答案,找出錯誤並理解錯誤的原因。
-
觀看教學影片: 許多教育平台(如 YouTube、均一教育平台)都有提供免費的小數點除法教學影片,透過視覺化的方式幫助理解。
-
實際應用練習: 將小數點除法應用到日常生活中,例如計算食譜的份量調整、商品打折後的價格、平均花費等,讓學習更具趣味性與實用性。
常見問題 (FAQ)
如何判斷小數點除法何時結束?
小數點除法通常會在兩種情況下結束:一是當除法計算到最後,餘數為零時,表示得到了一個有限小數;二是當題目要求將結果四捨五入到指定的小數點位數時,計算到該位數後即可結束,進行四捨五入;另外,如果發現計算過程中餘數開始重複出現,則表示商數將會是無限循環小數,此時可以停止並標記循環節。
為何小數點除法中要將除數化為整數?
將除數化為整數是為了簡化計算過程,使其變成我們更熟悉的整數除法。當除數是小數時,直接進行長除法會比較複雜且容易出錯。透過將除數和被除數同時乘以10的倍數(10, 100, 1000…)來移動小數點,可以保持除法運算原有的比例關係不變,確保結果正確。
小數點除法中商數的小數點如何定位?
在進行長除法時,當您從被除數中處理到原本小數點的位置時,就需要在商數(答案)的相同垂直位置上點上小數點。簡單來說,就是「被除數的小數點在哪,商數的小數點就跟著在哪」。
除不盡的小數點除法該怎麼辦?
對於除不盡的小數點除法(即餘數永遠不為零),其結果可能是無限循環小數。處理方式取決於具體要求:如果需要精確值,可以將其表示為分數;如果要求近似值,則通常會根據題目的指示,將結果四捨五入到指定的小數點位數,例如「四捨五入到小數點後第二位」。
小數點除法在日常生活中哪裡會用到?
小數點除法在日常生活中應用非常廣泛,例如:計算商品的單價(總價 ÷ 數量)、計算每公升油耗(總里程 ÷ 總油量)、分配食材份量(總份量 ÷ 人數)、換算匯率(總金額 ÷ 匯率)、計算平均分數、評估投資報酬率等。它是我們理解數量關係、進行精確計算的重要工具。
掌握小數點除法並非遙不可及的目標。透過理解其核心原理、熟練掌握基本步驟,並多加練習,您將會發現它比想像中更容易。希望這篇文章能為您提供清晰的指引,讓您在數學學習的道路上更進一步,充滿信心!