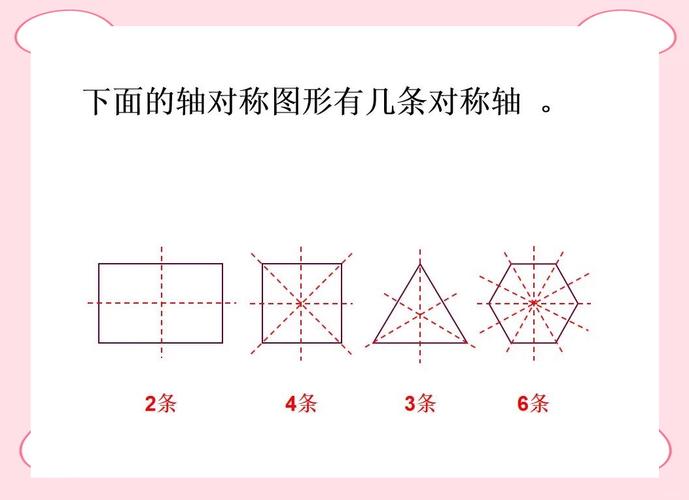
正六邊形有幾條對稱軸：全面解析其對稱之美

當我們談論正六邊形時，其完美的幾何結構總是令人著迷。許多人會好奇，這樣一個對稱的圖形究竟擁有多少條「對稱軸」？答案是六條。這篇文章將帶您深入探索正六邊形對稱軸的奧秘，理解這六條線如何賦予它獨一無二的平衡與美感。

什麼是對稱軸？

在幾何學中，一條對稱軸（或稱反射軸）是指一條能夠將圖形分成兩個完全相同的鏡像部分的直線。當我們沿著這條線將圖形對摺時，兩部分將會完全重疊。對稱軸的數量直接反映了一個圖形的對稱程度，對稱軸越多，圖形通常就越「平衡」或「規律」。

以最簡單的例子來說：

• 一個圓形有無數條對稱軸，因為任何穿過圓心的直線都是其對稱軸。
• 一個正方形有四條對稱軸：兩條連接相對頂點，兩條連接相對邊的中點。
• 一個等腰三角形只有一條對稱軸，它連接頂角與底邊中點。

理解了對稱軸的基本概念後，我們就可以更深入地探討正六邊形為何擁有其獨特的六條對稱軸。

正六邊形有幾條對稱軸？詳解六條對稱軸的分類

正六邊形總共有六條對稱軸，這六條軸可以根據它們穿過正六邊形的方式，分為兩大類：

第一類：通過相對頂點的對稱軸（3條）

這類對稱軸穿過正六邊形中心點，並連接兩個相對的頂點。由於正六邊形有六個頂點，每兩個相對的頂點可以確定一條直線，因此可以形成三條這樣的對稱軸。

想像一下，如果我們將一個正六邊形標記為A、B、C、D、E、F六個頂點（順時針），那麼這三條對稱軸將分別是：

• AD連線： 這條線穿過頂點A和頂點D。
• BE連線： 這條線穿過頂點B和頂點E。
• CF連線： 這條線穿過頂點C和頂點F。

沿著這三條中的任一條線對摺，正六邊形的兩半都會完美重疊。它們如同切割披薩的刀痕，將六邊形均等地分成兩份，展現出其完美的反射對稱性。

第二類：通過相對邊中點的對稱軸（3條）

另一類對稱軸同樣穿過正六邊形的中心點，但它們是連接兩條相對邊的中點。正六邊形有六條邊，每兩個相對的邊可以確定一條直線（通過其中點），所以也能形成三條這樣的對稱軸。

具體來說，這三條對稱軸將會是：

• 連接AB邊中點與DE邊中點的線。
• 連接BC邊中點與EF邊中點的線。
• 連接CD邊中點與FA邊中點的線。

這些線同樣能夠將正六邊形精確地分成兩半，使得兩邊互為鏡像。它們的特性與第一類對稱軸同樣重要，共同構成了正六邊形的完整對稱體系。

將這兩類對稱軸的數量相加（3條 + 3條），我們就得到了正六邊形總共擁有的六條對稱軸。

為何正六邊形恰好有六條對稱軸？

一個正n邊形，通常會有n條對稱軸。

正六邊形之所以擁有六條對稱軸，是因為它是一個正多邊形，且其邊數為偶數。這是一個關於正多邊形對稱性的一般規律：

• 如果正n邊形的n是奇數（例如正三角形、正五邊形），則其對稱軸的數量為n條，且每一條對稱軸都會通過一個頂點和其相對邊的中點。例如，正五邊形有5條對稱軸。
• 如果正n邊形的n是偶數（例如正方形、正六邊形、正八邊形），則其對稱軸的數量也為n條。其中一半（n/2條）通過相對的頂點，另一半（n/2條）通過相對邊的中點。

正六邊形正是屬於後者，n=6為偶數，因此它有3條通過相對頂點的軸，以及3條通過相對邊中點的軸，總共組成了6條對稱軸。這種分佈方式展現了偶數邊正多邊形特有的對稱結構。

正六邊形對稱的獨特魅力

對稱軸與旋轉對稱

除了擁有六條反射對稱軸之外，正六邊形還具備六階旋轉對稱。這意味著如果我們將正六邊形圍繞其中心旋轉60度（360度/6），它將會與自身完美重合。這種重複重合的現象會發生六次，直到完成360度的完整旋轉。這兩種對稱性（反射對稱和旋轉對稱）共同賦予了正六邊形極高的對稱性和穩定性。

幾何學上的完美比例

正六邊形還有一個有趣的特性：它可以完全由六個等邊三角形組成，這些三角形的共同頂點位於六邊形的中心。每個等邊三角形的邊長都等於正六邊形的邊長。這也解釋了為何其對稱軸能夠如此清晰地通過中心點並延伸至頂點或邊的中點，因為這些點是構成這些等邊三角形的關鍵元素。

正六邊形對稱軸的實際應用

正六邊形的完美對稱性不僅存在於數學教科書中，更廣泛地存在於我們的自然界和人造設計中，其六條對稱軸所帶來的力學優勢和美學價值被廣泛應用：

• 蜂巢： 蜜蜂建造的蜂巢單元就是完美的正六邊形結構。這種結構不僅能最大化儲存空間，還能以最少的蠟量提供最大的強度和穩定性，這正是其六條對稱軸所帶來的均勻受力與穩定性。
• 螺母和螺栓： 許多螺母和螺栓的頭部設計成正六邊形，方便扳手操作，且能均勻分散受力。其六邊形的設計使其在不同角度都能被有效轉動。
• 雪花： 大多數雪花結晶都呈現出六角星的形態，這是水分子結構在低溫下自然排列的結果，其精緻的六重對稱令人驚嘆。每一片雪花都是獨特的藝術品，但絕大多數都遵循著六條對稱軸的規則。
• 建築與設計： 正六邊形也被廣泛應用於建築設計、藝術圖案、瓷磚鋪設等領域，因為它具有良好的密鋪性，能夠無縫地填滿平面，形成和諧且堅固的結構。

總結

至此，您應該對正六邊形有幾條對稱軸有了非常清楚的認識。答案是六條，其中三條連接相對的頂點，另外三條連接相對邊的中點。這六條對稱軸共同構建了正六邊形獨特的平衡與美感，使其成為幾何學中一個特別而迷人的存在。

從微觀的原子結構到宏觀的自然景觀，正六邊形的對稱無處不在，它不僅是數學上的嚴謹，更是大自然設計智慧的體現。下次當您看到一個正六邊形時，不妨試著在腦海中勾勒出它的六條對稱軸，感受這份隱藏在圖形中的幾何力量。

常見問題 (FAQ)

如何判斷一個圖形有多少條對稱軸？

判斷一個圖形有多少條對稱軸，最直觀的方法是想像沿著一條線將圖形對摺，看兩邊是否能完全重疊。如果能完美重疊，那條摺痕就是一條對稱軸。對於正多邊形，一個正n邊形通常有n條對稱軸；對於其他不規則圖形，則需要逐一檢查所有可能的反射線。

為何正五邊形只有五條對稱軸？

正五邊形作為一個正奇數邊多邊形，其每一條對稱軸都通過一個頂點以及其對面那條邊的中點。由於有五個頂點（和五條邊），因此總共有五條對稱軸。由於邊數為奇數，它不存在像偶數邊多邊形那樣，有通過相對邊中點的對稱軸。

正六邊形的所有對稱軸都經過中心點嗎？

是的，正六邊形的所有六條對稱軸都一定會經過其幾何中心點。這是所有正多邊形的一個重要特性：無論是通過相對頂點還是相對邊中點的對稱軸，它們都會相交於該正多邊形的中心。

如何徒手繪製正六邊形的對稱軸？

您可以先找到正六邊形的三對相對頂點，然後用尺子連接它們；這就是其中三條對稱軸。接著，找到三對相對邊的中點，並用尺子連接它們；這就是另外三條對稱軸。所有這六條線段都會精確地交於正六邊形的中心點。

為何蜂巢是正六邊形而不是正方形或正三角形？

正六邊形是能夠完全密鋪平面且相同面積下周長最短（即材料最省）的三種正多邊形（正三角形、正方形、正六邊形）中，最接近圓形的形狀，這使得它在有限的空間內儲存更多內容。同時，其結構在承受多方向壓力時更為穩定，達到最佳的效率和強度，這與其多條對稱軸帶來的平衡性息息相關，使得蜂巢的構造既經濟又堅固。