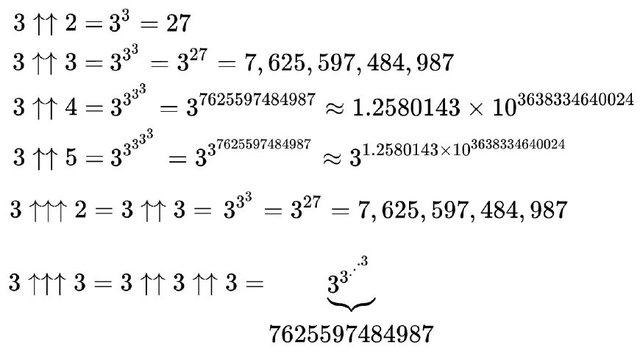葛立恆數有幾位?深入探索這個宇宙級巨大數的奧秘與其不可思議的規模
Table of Contents
葛立恆數有幾位?深入探索這個宇宙級巨大數的奧秘與其不可思議的規模
你曾否在夜深人靜時,抬頭仰望星空,然後心底突然冒出一個問題:「宇宙到底有多大?最大、最不可思議的數字又是什麼?」或許,在一次偶然的機緣下,你聽說過「葛立恆數」(Graham’s Number)這個名字,然後不禁好奇:這個號稱是數學界最大巨獸的數字,它究竟有幾位呢?
好吧,別賣關子了,讓我直接給您一個快速且精確的答案:葛立恆數是一個無法用「位數」來衡量的數字,它的規模遠遠超越了任何我們能寫下、甚至能想像的位數。我們無法計算出它確切的位數,因為即使是「表示它有多少位」這個數字,本身就已經是一個超級巨大的數字了。這麼說吧,即使你把整個可觀測宇宙中所有的原子都拿來當作儲存空間,也遠遠不足以寫下這個數字的所有位數。它就是這麼地、這麼地、這麼地大!不過,儘管如此,我們倒是知道它的最後一位數字是7。是不是很神奇呢?
葛立恆數:一個連科學家都感到震驚的數字
葛立恆數,英文名為 Graham’s Number,是由美國數學家羅納德·葛立恆(Ronald Graham)在1977年提出的一個巨大數字。它並不是為了「大」而大,而是作為一個上界,在數學的「拉姆齊理論」(Ramsey Theory)中的一個特定問題證明中被提出。具體來說,這個問題是關於高維超立方體的邊緣染色的,需要找出最小的維度 N,使得對 N 維超立方體的所有邊進行兩種顏色染色後,必定存在一個單色完全子圖。葛立恆數就是這個 N 值的一個上界,而且是當時在數學證明中出現過的最大數字,因此被《金氏世界紀錄大全》所收錄,雖然現在已經有一些更大的數字被提出(我們後面會提到)。
在我看來,葛立恆數之所以引人入勝,不僅僅是因為它的規模,更是因為它所代表的數學思維極限。它迫使我們重新思考數字的定義,以及我們如何去表達那些超越日常經驗的量。每一次向學生或朋友解釋它時,我總能感受到他們從好奇到震驚,再到一種近乎敬畏的眼神,這種過程本身就很有趣。
究竟是什麼讓葛立恆數如此巨大?從基礎的數學符號談起
要理解葛立恆數為何如此龐大,我們必須先從最基本的數學運算符號開始,然後一步步地向上攀升,直到超越我們平常所能理解的極限。
挑戰指數爆炸:Knuth箭頭符號的登場
我們從小學數學就認識加法、乘法。乘法是重複的加法(例如 3 × 4 = 3 + 3 + 3 + 3)。而指數運算,也就是「次方」,則是重複的乘法(例如 34 = 3 × 3 × 3 × 3)。光是指數運算就已經能製造出驚人的巨大數字了,不是嗎?想想 210 是 1024,2100 就已經是一個有 31 位的數字了,而 21000 更是有 302 位!但這離葛立恆數還差了十萬八千里。
為了表達比指數運算更快的增長速度,數學家唐納德·高德納(Donald Knuth)在1976年發明了高德納箭頭符號(Knuth’s up-arrow notation),或稱Knuth上箭號表示法。這個符號將運算層級進一步推高:
- 單箭頭 (↑):指數運算
- a ↑ b = ab
- 例如:3 ↑ 4 = 34 = 81
- 雙箭頭 (↑↑):超冪(tetration),重複的指數運算
- a ↑↑ b = aaa…a (b 個 a)
- 例如:3 ↑↑ 4 = 3333。讓我們來算算看:
- 33 = 27
- 327 = 7,625,597,484,987 (一個有 13 位的數字)
- 37,625,597,484,987 = 哇!這已經是一個天文數字了!這個數字的位數約等於 7.6 兆。光是想像一個數字有 7.6 兆個位數,就已經開始感到頭暈目眩了,不是嗎?
- 三箭頭 (↑↑↑):超冪的重複,稱為 pentation
- a ↑↑↑ b = a ↑↑ (a ↑↑ (… a ↑↑ b)) (b 個 a↑↑)
- 例如:3 ↑↑↑ 2 = 3 ↑↑ 3 = 333 = 327 = 7,625,597,484,987
- 而 3 ↑↑↑ 3 呢?它就等於 3 ↑↑ (3 ↑↑ 3) = 3 ↑↑ (7,625,597,484,987)。這個數字的規模已經不是用位數來表達,而是用「位數的位數」來表達了!
- 四個箭頭 (↑↑↑↑):以此類推,重複的 pentation,稱為 hexation,等等…
Knuth箭頭符號的精髓在於,當箭頭的數量增加時,數字的增長速度會以一個「難以理解」的速度暴漲。一個小小的變化,就能讓數字從「大」變成「無法想像的大」。
超越箭頭的限制:葛立恆數的定義過程
好了,現在我們知道 Knuth 箭頭符號的威力了。但葛立恆數的定義,卻比固定箭頭數的符號更為複雜,它需要箭頭的數量本身也以驚人的速度增長。葛立恆數 G 被定義為一個序列 G1, G2, …, G64 的最後一項,也就是 G64。這個序列的定義步驟如下:
- 定義 G1:
- G1 = 3 ↑↑↑↑ 3
- 這就是 3 四個箭頭 3。請記住,這已經是一個無法想像的巨大數字了!它代表 3 以超冪的方式疊加了 3 次,而每次疊加的「層數」本身又是 3。用數學語言來說,3 ↑↑↑↑ 3 = 3 ↑↑↑ (3 ↑↑↑ 3)。這是一個幾乎不可能具體想像的數字。
- 定義 G2:
- G2 = 3 ↑G1 3
- 這裡的「↑G1」表示箭頭的數量是 G1 個!是的,您沒聽錯,箭頭的數量不再是固定的 4 個,而是 G1 個!而 G1 本身已經是我們無法想像的巨大數字了。這意味著 G2 是 3 與 3 之間,有 G1 這麼多個箭頭運算。天啊,光是 G1 個箭頭,就足以讓整個宇宙瞬間蒸發,如果我們真能把它算出來的話。
- 定義 G3:
- G3 = 3 ↑G2 3
- 現在,箭頭的數量變成了 G2 個!G2 比 G1 不知道大了多少個「層級」,而現在箭頭的數量又變成了 G2!這個遞迴定義以一種爆炸性的方式增長著數字的規模。
- 以此類推,直到 G64:
- Gk = 3 ↑Gk-1 3 (對於 k > 1)
- 葛立恆數 G 就是這個序列的第 64 項,也就是 G64。
這就是葛立恆數的定義,它之所以如此巨大,是因為它的定義方式是「自指」的——前一個數字決定了下一個數字的「表達複雜度」本身。每一步都將數字推向一個新的、更不可思議的規模。這就好比你試圖用一個數字來表達另一個數字的位數,然後又用那個位數來表達另一個數字的位數,如此反覆 64 次。我個人覺得,這種抽象的增長方式本身就充滿了美感,它展現了數學如何能超越我們直覺的理解。
為什麼我們無法「數」出葛立恆數的位數?
現在,您應該能理解為什麼葛立恆數的位數是無法被具體計算或寫出來的了。原因很簡單,但卻非常深刻:
- 位數的爆炸性增長: 我們知道 G1 已經是一個極其龐大的數字,其位數本身就是個天文數字。而 G2 則是用 G1 作為箭頭數量來定義的。這意味著 G2 的位數,將會是與 G1 類似規模的數字。舉個簡化的例子:如果一個數字 A 有 M 個位數,那麼 A 的位數,log10 A,約等於 M。但如果一個數字 B = a ↑A b,它的位數會是天文數字。
- 儲存與表達的限制: 即使我們只計算 G1 的位數,這個位數本身就已經大到無法寫下,因為它遠遠超過了可觀測宇宙中所有原子數量的總和。更何況 G2 的位數,G3 的位數… 一直到 G64 的位數。沒有任何物理介質,無論是紙張、電腦硬碟,還是宇宙中的基本粒子,能夠儲存這個數字的所有位數。
- 超越數學工具的極限: 雖然我們可以利用模運算(Modular Arithmetic)來計算葛立恆數的最後幾位數字(比如我們知道最後一位是 7),但這並不意味著我們能處理整個數字。模運算只能告訴我們數字的「餘數」模式,而無法揭示它的整體規模。這就好比你知道一條河流的終點在海邊,但你無法因此得知這條河有多長、有多寬、流速多快。
因此,當有人問「葛立恆數有幾位」時,我的答案總是:「它的位數本身就是一個超乎想像的數字,大到我們根本無法用任何已知的符號或概念來表達。想像一下,如果你要計算宇宙中所有沙子的數量,然後用這個數字來表示另一個數字的位數,葛立恆數的規模還要遠遠超出這個例子無數倍。」這真的讓人感到人類的認知邊界是多麼的渺小啊!
葛立恆數的應用與它在數學界的地位
葛立恆數雖然大得嚇人,但它在數學界可不是徒有虛名,它承載著重要的數學意義和啟發性:
- 拉姆齊理論的具體證明: 它是拉姆齊理論中一個特定問題的上界證明。在數學中,找到一個問題的「上界」或「下界」至關重要,它們幫助我們理解問題的範圍和複雜性。葛立恆數的出現,證明了即使是看似簡單的問題,也可能需要如此龐大的數字才能描述其邊界。
- 啟發了巨大數的研究: 葛立恆數的提出,激發了數學家們對其他超大數字的探索和定義。它證明了人類的抽象思維能力可以超越物理世界的限制,去構建和理解那些無法具體體驗的巨大概念。
- 計算機科學的極限挑戰: 儘管我們無法計算出葛立恆數本身,但它也提醒了我們在設計算法和數據結構時,數字的規模可能遠超預期。對於某些組合問題,即使是「小型」的輸入,其輸出也可能迅速膨脹到葛立恆數的級別,這對計算機處理能力提出了極大的挑戰。
從我的個人經驗來看,每當我談論葛立恆數時,它總能引發聽眾對數學的深層思考。它不僅僅是一個數字,更是一個哲學問題——它讓我們思考「無限」與「可數」的邊界,思考人類心智如何能夠創造和理解超越其感官經驗的事物。這種對抽象極限的探索,正是數學魅力所在。
葛立恆數與其他巨大數的比較
當然,葛立恆數在歷史上曾是「金氏世界紀錄」上最大的數字,但隨著數學的發展,也出現了一些比葛立恆數還要大的數字。不過,葛立恆數依然是許多人談論巨大數時的第一印象。為了讓您對數字的規模有一個更清晰的認識,我們來看看它和其他一些著名巨大數的比較:
請注意,以下表格只是為了方便理解,實際的比較會非常複雜,因為這些數字的增長機制各不相同。有些數字甚至難以用 Knuth 箭頭符號來表達。
| 巨大數名稱 | 簡要描述/表達方式 | 規模(相對) |
|---|---|---|
| 古戈爾 (Googol) | 10100 (1後面跟100個零) | 非常大,但很容易寫出。 |
| 古戈爾普勒克斯 (Googolplex) | 10Googol (1後面跟Googol個零) | 比宇宙中的原子數量還要多,無法寫出所有位數,但可以用指數塔表示。 |
| Skewes’ Number (斯丘斯數) | 第一種:eee79;第二種:eeee7.705 | 天文數字,比Googolplex大很多,需要指數塔來表達。 |
| Moser’s Number (莫澤數) | 以多邊形鏈定義,比簡單的Knuth箭頭表達更複雜。 | 比葛立恆數略小,但仍遠遠超過Skewes’ Number。已經需要更高級的數學表示法。 |
| 葛立恆數 (Graham’s Number) | G64,遞迴定義為 Gk = 3 ↑Gk-1 3 | 極其龐大,無法用傳統的指數塔或固定箭頭數的Knuth符號表達。 |
| TREE(3) | 基於樹圖的一個組合數學函數。 | 比葛立恆數大到無法想像,甚至遠超許多比葛立恆數更大的數。 |
| Rayo’s Number (雷約數) | 基於一階集合論的表達能力。 | 概念上比TREE(3)還要大,涉及到邏輯語言的計算能力。 |
從這個表格中您可以看到,葛立恆數是一個「分水嶺」。在它之前,數字雖然巨大,但大多還能用不斷堆疊的指數(即指數塔)或固定箭頭數的 Knuth 符號來表達。但葛立恆數一出現,就直接將箭頭的數量本身也變成了一個超乎想像的數字,這使得它的增長速度躍升到一個全新的層次。而之後出現的 TREE(3) 等數字,更是使用了完全不同的、更為抽象的數學定義方式,它們的規模甚至讓葛立恆數顯得「微不足道」。
這一切都告訴我們,數字的世界是如此的廣闊無垠,遠遠超出了我們日常生活的體驗。作為一個數學愛好者,我常常為這種概念上的無窮性感到震撼,它提醒我們宇宙和數學的奧秘是多麼的深不可測。
讀者常見問題與專業解答
葛立恆數的價值在哪裡?它只是個大數字嗎?
當然不是!葛立恆數的價值遠遠超出了它作為一個「大數字」本身。它的核心價值在於它在數學證明中的應用。
它作為拉姆齊理論(Ramsey Theory)中一個特定問題的「上界」而誕生。拉姆齊理論是組合數學的一個分支,研究的是在足夠大的結構中,必然會出現某種特定性質的子結構。這個理論充滿了「無限大」和「必然存在」的美感。
葛立恆數的出現,實際上是為了解決一個關於高維超立方體染色的問題:需要找到一個最小的維度 N,使得無論怎麼對這個 N 維超立方體的邊進行兩種顏色染色,都必然存在一個單色的 K4 (四個點的完全圖)。葛立恆數就是這個 N 的一個上界,證明了這樣的 N 是存在的。這項證明不僅推動了拉姆齊理論的發展,也展現了數學家們在抽象思維和證明複雜概念方面的能力。
此外,葛立恆數也作為一個重要的里程碑,啟發了對「巨大數」的更深入研究,並擴展了我們對數字表達方式的理解,例如 Knuth 箭頭符號等。它提醒了我們,即使在純粹的數學領域,也有著遠超人類直觀感受的龐大存在。
我們知道葛立恆數的最後一位數字是什麼嗎?
是的,這是一個很棒的問題!儘管我們無法計算出葛立恆數的全部位數,但透過精巧的模運算(Modular Arithmetic),數學家們確實能夠推算出葛立恆數的最後一位數字。
答案是:葛立恆數的最後一位數字是7。
這是怎麼做到的呢?關鍵在於指數的週期性。當我們計算一個數字的冪次方時,其尾數往往會呈現出週期性的變化。例如,以3為底數的冪次方:
- 31 = 3
- 32 = 9
- 33 = 27 (尾數是7)
- 34 = 81 (尾數是1)
- 35 = 243 (尾數是3)
您會發現,3的冪次方的尾數遵循一個週期:3, 9, 7, 1, 3, 9, 7, 1… 這個週期是4。透過更複雜的模運算和指數塔的性質,數學家能夠確定葛立恆數在模10下的值,從而得到它的最後一位數字是7。這種技巧展示了即使面對無法想像的巨大數字,數學仍然能提供工具來揭示其某些屬性。
有沒有比葛立恆數更大的數字?
絕對有!數學的世界是無限的,沒有什麼是「最大」的。葛立恆數在1977年被提出時,確實是當時已知的在數學證明中出現過的最大數字,這讓它聲名大噪。
然而,隨著時間的推移和數學的發展,特別是在組合數學和計算機理論中,已經有更多被定義出來的數字比葛立恆數還要龐大得多。其中最著名的幾個例子包括:
- TREE(3): 這個數字來自於圖形理論中的一個簡單遊戲,它以驚人的速度增長。TREE(3) 比葛立恆數大到一個無法想像的程度,甚至可以說葛立恆數在它面前微不足道。要理解 TREE(3) 的定義需要一些圖論知識,但其核心思想是關於無標記樹的序列。
- Rayo’s Number (雷約數): 這個數字的定義更為抽象,它涉及到一階集合論的表達能力。簡而言之,Rayo’s Number 是在特定語言中,能被一個特定長度語句定義出的最大有限數。它的規模甚至遠超 TREE(3),已經進入了計算複雜性和邏輯學的領域。
- Busy Beaver Numbers (忙碌海狸數): 這是一類數字,其中 BB(n) 是指一個有 n 個狀態的圖靈機能夠在停機前寫下的最大非零符號數。BB(n) 的增長速度非常快,BB(5) 就已經是個巨大數,而 BB(6) 更是超出人類的理解範圍,它的增長速度被認為比任何可計算的函數都快。
這些數字的出現不斷地拓寬了我們對「大」的認知極限。我的個人看法是,這其實挺酷的,它證明了數學世界總有新發現,總有更深的奧秘等待我們去探索。葛立恆數只是這趟奇妙旅程中的一個重要地標,而不是終點。
葛立恆數是如何被「發現」的?
葛立恆數並非像行星或新物種那樣被「發現」的,它更像是被「構造」或「定義」出來的。它的誕生背景是嚴肅的數學研究,特別是在拉姆齊理論(Ramsey Theory)中。
在1970年代,羅納德·葛立恆教授與布魯斯·李布(Bruce Rothschild)合作,研究一個關於高維超立方體的問題。這個問題是這樣的:想像一個 n 維超立方體,它的每個頂點都連接著其他頂點,形成一個巨大的圖形。現在,我們把這個超立方體的每一條邊都塗上兩種顏色(比如紅色和藍色)。問題是,N 必須至少多大,才能保證無論我們怎麼染色,總能找到一個單色的 K4(一個有四個頂點且所有邊同色的完全圖)?
葛立恆教授在解決這個問題的過程中,需要找到一個足夠大的數字作為這個 N 的上界,以證明這樣的 N 是存在的。最終,他在1971年發表了證明,並在這個證明中用到了葛立恆數作為上界。後來,在1977年,馬丁·加德納(Martin Gardner)在《科學美國人》(Scientific American)雜誌上介紹了這個數字,使其廣為人知,並稱之為葛立恆數。
所以,葛立恆數不是從數據中「提取」出來的,也不是透過物理實驗「測量」出來的,而是在純粹的數學邏輯推導和證明過程中,根據需要被「建構」出來的一個數字。它的存在證明了即使是最抽象的數學問題,也可能需要超乎想像的巨大數字來進行描述和理解。