珠算可以算乘法嗎：深度揭秘珠算乘法的奧秘與實踐技巧

前陣子，我的小姪子拿著他新買的小算盤跑來問我：「叔叔，這個算盤除了加減法，連乘法也算得出來嗎？是不是只有很厲害的人才辦得到啊？」看到他半信半疑又充滿好奇的眼神，我忍不住笑了出來，心想這正是許多人對珠算的誤解與迷思呢！今天，就讓我來跟大家好好聊聊這個話題，帶大家一窺珠算乘法的奧秘。

快速解答：珠算究竟能不能算乘法？

答案是：當然可以！而且珠算不只可以算乘法，就連除法、開平方、開立方等複雜的運算都能輕鬆駕馭。事實上，在電子計算器普及之前，珠算就是人類進行各種複雜計算最主要且最有效率的工具之一。它並不是什麼神祕的魔法，而是一套嚴謹且邏輯性極強的計算系統，只要掌握了其原理與技巧，任何人都能透過算盤算出乘法。

珠算之所以能進行乘法，主要是透過「分解」與「累加」的原理。我們將乘數和被乘數的每一位數逐一相乘，然後根據位值將這些「部分積」準確地累加到算盤的特定位置上，最終得到總乘積。這就像我們手寫長乘法一樣，只不過在算盤上，所有的步驟都是具體地在珠子移動中完成，視覺化且有條不紊。

珠算乘法的歷史淵源與獨特魅力

珠算，作為一種古老的計算工具與技術，其歷史可以追溯到數千年前。從古巴比倫的沙盤算、羅馬的溝槽算盤，到中國獨特的珠算盤，算盤的演變見證了人類對數字與計算的追求。特別是中國的珠算，以其結構簡潔、操作靈活的特點，在東亞地區廣泛流傳，成為數百年來商賈、會計、學子不可或缺的技能。

在過去，一個熟練的珠算高手，其計算速度甚至能與早期的機械計算器媲美。這種將複雜計算化繁為簡的能力，不僅大幅提升了商業交易的效率，也為科學研究提供了可靠的計算基礎。對我個人來說，珠算乘法最迷人的地方，不僅在於它能迅速得出結果，更在於它訓練了心算能力，提升了數字敏感度。那種指尖撥動珠子、數字在腦中跳躍的過程，本身就是一種獨特的數學美學體驗。

珠算乘法的基本原理：拆解與整合的藝術

要了解珠算乘法，我們首先要明白它的核心思路其實與我們手寫的長乘法（直式乘法）是異曲同工的。手寫乘法是將一個數字乘以另一個數字的每一位，然後將結果錯位相加；珠算乘法也是如此，只是所有的中間步驟都在算盤上透過珠子的移動來完成。

核心概念：乘法口訣與位數對應

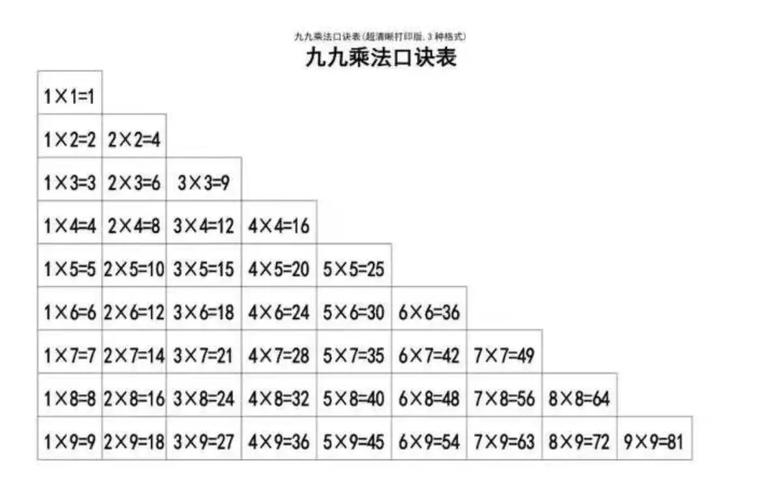
珠算乘法的基礎，毫無疑問就是我們從小背到大的「九九乘法口訣」。如果連基本的乘法口訣都不熟悉，那麼無論是手算還是珠算，都會寸步難行。在珠算中，我們將乘數和被乘數分解成單一位數的乘積，然後再將這些單一位數的乘積，根據其所處的「位值」正確地放置到算盤上並累加。

舉例來說，當我們計算 23 乘以 45 時，其實就是將 (20 + 3) 乘以 (40 + 5)。珠算會逐位進行，比如先計算 3 乘以 5 的個位數，再考慮 3 乘以 4 的十位數，然後是 2 乘以 5 的十位數，以及 2 乘以 4 的百位數。每一個小乘積，都必須精確地對應到算盤上的正確位數。

準備工作：算盤的設置與手指的協調

在進行珠算乘法之前，有幾個基本的準備工作和習慣養成是非常重要的：

• 清盤歸零： 每次計算前，務必將算盤上的所有珠子撥回到原始位置（上珠向上、下珠向下），確保算盤是「空的」，避免產生錯誤。
• 定位基準點： 在算盤上設定一個固定的「個位」位置。通常會選擇算盤中間某一檔作為個位，並在其左側的檔位作為十位、百位、千位等，右側則為小數點後的位數。這樣有助於在計算過程中保持位值清晰。
• 熟練指法： 珠算非常講究指法。撥動珠子主要使用右手拇指和食指，拇指撥上珠或下珠向上，食指撥下珠向下或上珠向下。熟練的指法能讓撥珠動作更流暢、更迅速，減少錯誤。

這點我必須強調，尤其對於初學者來說，指法的練習和位值的概念是重中之重。沒有正確的指法，速度上不去；沒有清晰的位值概念，結果就會一團亂。

珠算乘法的實踐步驟：以「直乘法」為例

珠算乘法的方法有多種，其中最常見且相對容易上手的是「直乘法」，也稱作「單向乘法」或「一位乘一位直接相乘法」。這種方法與我們手寫的直式乘法思路最接近，非常適合初學者理解。

範例說明：23 x 45

我們就以一個簡單的例子：23 乘以 45，來詳細說明珠算直乘法的步驟。

1. 設定乘數與被乘數：

   首先，在算盤上預留足夠的空間放置結果，通常是乘數位數 + 被乘數位數的檔位。然後，我們將乘數和被乘數設定在算盤上。假設我們從左到右數，第11檔為結果的個位。

   將被乘數 23 設定在算盤的左側，例如，將「2」設定在第3檔，「3」設定在第4檔。將乘數 45 設定在被乘數的右側，例如，將「4」設定在第6檔，「5」設定在第7檔。

2. 從高位開始乘：被乘數的最高位乘以乘數的最高位

   我們從被乘數的最高位「2」開始，乘以乘數的最高位「4」。

   • 「2」乘以「4」等於「8」。
   • 由於 2 是在十位（第3檔），4 也是在十位（第6檔），所以這個「8」應該放在百位的位置。
     在我們預留的結果區，從第3檔（被乘數的最高位所在檔）和第6檔（乘數的最高位所在檔）的總和減去一個位置，也就是第3 + 第6 – 1 = 第8檔。將「8」加到第8檔。
   • 算盤現在顯示：左側是 23，中間是 45，然後結果區有了 8。
3. 繼續高位乘以低位：被乘數的最高位乘以乘數的次高位

   接著，我們用被乘數的最高位「2」去乘以乘數的次高位「5」。

   • 「2」乘以「5」等於「10」。
   • 同樣地，2 是在十位（第3檔），5 是在個位（第7檔），所以這個「10」中的「1」應該放在百位，「0」放在十位。
     其結果的個位應該從第3 + 第7 – 1 = 第9檔開始。也就是將「1」加到第9檔的左邊，即第8檔，並將「0」加到第9檔。
   • 此時第8檔的8要加上1變成9。第9檔是0。
   • 算盤結果區顯示：90。
4. 處理被乘數的次高位：被乘數的次高位乘以乘數的最高位

   現在輪到被乘數的次高位「3」了，它乘以乘數的最高位「4」。

   • 「3」乘以「4」等於「12」。
   • 3 是在個位（第4檔），4 是在十位（第6檔），所以這個「12」中的「1」應該放在十位，「2」放在個位。
     其結果的個位應該從第4 + 第6 – 1 = 第9檔開始。也就是將「1」加到第9檔，並將「2」加到第10檔。
   • 此時第9檔的0要加上1變成1。第10檔是2。
   • 算盤結果區顯示：90 + 12 = 102。
5. 處理被乘數的次高位：被乘數的次高位乘以乘數的次高位

   最後，用被乘數的次高位「3」去乘以乘數的次高位「5」。

   • 「3」乘以「5」等於「15」。
   • 3 是在個位（第4檔），5 也是在個位（第7檔），所以這個「15」中的「1」應該放在十位，「5」放在個位。
     其結果的個位應該從第4 + 第7 – 1 = 第10檔開始。也就是將「1」加到第10檔，並將「5」加到第11檔。
   • 此時第10檔的2要加上1變成3。第11檔是5。
   • 算盤結果區顯示：102 + 15 = 1035。
6. 完成計算並讀取結果：

   所有的部分積都累加完畢，算盤上最終顯示的結果就是乘積。在本例中，您會在算盤的結果區看到「1035」。

是不是覺得有點複雜？這是因為文字描述會將原本同步進行的動作拆解開來。實際上，熟練的珠算者在撥珠的過程中，會非常流暢地完成這些步驟，而不是像機器人一樣一步一步思考。關鍵在於對位值的精確把握和對乘法口訣的反射性應用。

深入技巧：零的處理與特殊情況

在珠算乘法中，處理「0」是一個小小的眉角。當乘數或被乘數中含有「0」時，例如 20 x 45，我們知道 2 乘以 0 就是 0。在算盤上，這意味著該位數「不用撥珠」或者「撥零珠」。但最重要的還是要記住這個「0」所代表的位值，避免因忽略而導致位數錯亂。熟能生巧，多練習自然能掌握這些細節。

珠算乘法與現代計算工具的比較：誰勝誰負？

隨著科技的進步，電子計算器、電腦甚至手機應用程式都能在彈指之間完成複雜的計算。那麼，學習珠算乘法在現代社會還有意義嗎？這得從不同的角度來看。

速度與效率：人腦與機器的競賽

從純粹的速度和處理大規模複雜計算的效率來看，人類的珠算能力當然無法與現代電子計算工具相比。一台幾百塊錢的計算器，就能在幾秒內算出天文數字的乘積，而且幾乎零失誤。這是人類大腦和手指無論如何都無法超越的。

但是，這並不代表珠算就此失去價值。在某些特定情境下，例如需要快速估算、沒有電子設備的場合，或者對於培養個人心算能力而言，珠算依然有其獨到的優勢。它的「零誤差」特性（只要操作正確），也是機械計算器所不具備的「物理驗證」過程。

認知發展與教育價值：珠算獨特的優勢

我個人認為，珠算最大的價值，其實體現在其對人腦認知能力的開發與訓練上。許多教育研究都指出，學習珠算對兒童的智力發展有著顯著的正面影響。以下幾點是珠算無可取代的優勢：

• 提升專注力： 珠算要求計算者高度集中精神，稍有分心就容易出錯。長期練習能有效訓練專注力。
• 強化記憶力： 珠算在進行心算時，需要在大腦中「模擬」算盤撥珠的過程，這對短期記憶和空間記憶都是極佳的鍛鍊。
• 培養邏輯思維： 珠算步驟嚴謹，每一步都環環相扣，這有助於培養清晰的邏輯思考能力和問題解決能力。
• 增強數感： 長期接觸珠算，能讓學習者對數字的「量感」和位值概念有更深刻的理解，看到數字就能快速反應其大小和關係。
• 訓練手眼協調： 撥珠動作精準，需要手眼高度協調，對小肌肉發展也有助益。

在我觀察過的孩子中，那些有學習珠算的孩子，普遍在數學課堂上表現得更有自信，對於數字的敏感度也更高。他們在面對複雜計算時，思路往往比同齡人更清晰，這點是電子計算器無法提供的學習體驗。

精通珠算乘法的關鍵秘訣

如果看完這篇文章，您也對珠算乘法產生了興趣，甚至想親自嘗試學習，那麼以下幾個關鍵秘訣或許能幫助您事半功倍：

1. 熟練基本加減法： 珠算乘法的本質是多個加法的組合。如果加減法不熟練，乘法就更難搞定。
2. 精通乘法口訣： 這是最基礎的基礎，如同蓋房子前的地基。
3. 掌握位值概念： 計算過程中，每一個數位的精確定位是成功的關鍵。多練習數字的讀寫和位值轉換。
4. 大量練習： 珠算是一門技術活，沒有大量的練習就無法熟練。從簡單的兩位數乘一位數開始，逐步增加難度。
5. 保持耐心與專注： 初學珠算可能會覺得繁瑣，甚至有些挫敗感。千萬別急，慢慢來，享受撥珠的過程，成果自然會展現。

常見問題與專業解答

問：珠算乘法會比手算快嗎？

答：對於初學者來說，珠算乘法一開始可能不會比手寫的直式乘法快，因為您需要時間去熟悉算盤的撥珠技巧和位值轉換。然而，一旦您掌握了珠算的基本原理和熟練的指法，珠算的計算速度往往會遠超手寫計算。這是因為珠算提供了一種高度系統化和視覺化的操作介面，能夠幫助您更有效率地處理多位數的乘法。

珠算高手在進行心算時，他們的大腦會自動在「腦海中」浮現一個算盤，並進行虛擬的撥珠動作。這種訓練出來的心算能力，其速度和準確性是普通手算難以比擬的。所以，速度的提升是一個循序漸進的過程，取決於您的練習量和熟練度。

問：學習珠算乘法對小孩有什麼好處？

答：學習珠算乘法對小孩的好處是多方面的，遠不止於提高計算速度。首先，它能極大地提升孩子的專注力和記憶力。珠算要求孩子在計算過程中保持高度集中，長時間練習有助於培養良好的學習習慣。其次，它能強化孩子對數字的理解和數感，讓他們對位值、進位、退位等概念有更直觀的認識。

此外，珠算訓練還能促進左右腦的均衡發展。左腦負責邏輯思維，右腦則負責空間想像力。在珠算過程中，孩子既要進行邏輯推理，又要在大腦中建構算盤的空間影像，這對開發潛能非常有益。許多研究也指出，學習珠算的孩子在解決問題、空間推理和數學應用題方面的表現會更出色。

問：珠算乘法有其他方法嗎？

答：是的，珠算乘法確實存在不同的方法和技巧，雖然核心原理都是基於分解與累加。除了文中詳細介紹的「直乘法」（或稱「位數對齊法」），還有一些更進階或針對特定情境優化的方法，例如「隔位乘法」。

「隔位乘法」與直乘法在設定和撥珠上有些許不同，它允許乘積的各位數產生在不同的檔位上，再逐步調整。對於初學者，通常建議從直乘法開始學習，因為它的邏輯與手寫乘法最接近，容易理解。當掌握了基本功後，可以再探索其他珠算乘法技巧，甚至將其應用於更複雜的計算，如連乘、乘方等。

問：在現代社會，學習珠算乘法還有意義嗎？

答：當然有意義！儘管現代計算工具普及，但學習珠算乘法的價值已經從單純的「計算工具」轉變為「思維訓練工具」。正如前面提到的，它對專注力、記憶力、邏輯思維、數感和手眼協調的培養，是電子產品無法取代的。這些心智能力，不僅對學習數學有幫助，對於孩子未來的學習和工作都是寶貴的資產。

更重要的是，珠算也傳承了一種古老的文化和智慧。在追求高科技的同時，回歸傳統，體驗這種人類早期卓越的計算藝術，本身就是一種豐富的學習體驗。它不僅能培養耐心和毅力，還能讓學習者體會到解決問題的樂趣和成就感。所以，無論是作為一門興趣，還是作為一種提升個人心智能力的訓練，學習珠算乘法在現代社會依然具有其獨特的價值和意義。